Números infinitos
¿Infinito más grande?Si partimos de una teoría del Universo infinito podemos encontrar una explicación espacio-temporal, para los que estudian el Cosmos con sus grandes telescopios (Hubble) y están conscientes y claros que se trata de una parte limitada del espacio observable, pero con la convicción que hay otras cosas más allá, hasta el infinito.

Por aquí ya podemos ir definiendo el concepto de infinito, como el "campo" que no tiene límites, entendiendo por "campo" cualquier cosa que deseamos analizar, así hablamos del universo infinito, caos infinito o número infinito. Sin embargo, en el primer caso ya han aparecido nuevas teorías que sugieren que el Universo no es infinito, o nuevos cuestionamientos como lo expone el matemático Marcus du Sautoy acerca que los humanos nunca sabremos si el universo es infinito. Por el momento me limitaré a presentarles algunos números que pueden verse como una expresión matemática que sea más infinita que otra, ya ven que si pongo un límite a este artículo ya no me extenderé infinitamente en la explicación, jajaja!
¿Algoritmos hacia el infinito?
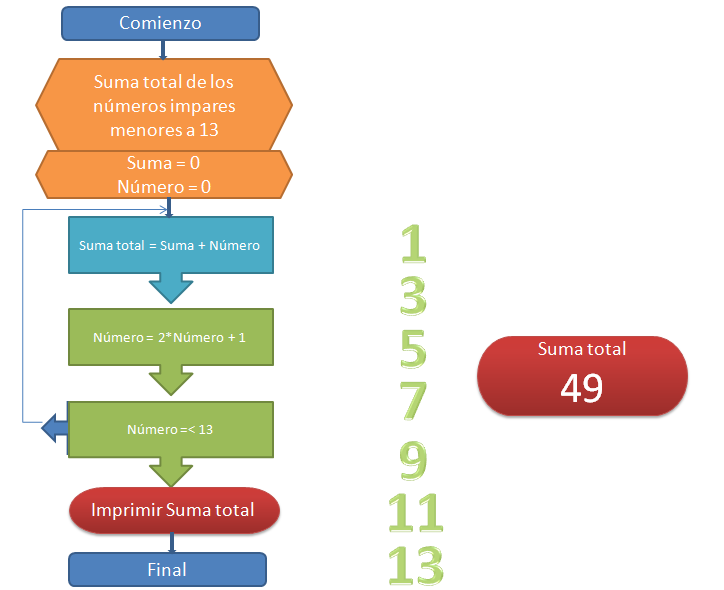
Es más, si seguimos desarrollando los números pares (2*n) y los números impares (2*n + 1) se verifica que realmente existe una cantidad ilimitada de este tipo de números que tiende al infinito (∞). Si ampliamos el espectro de números hacia el conjunto de los ENTEROS, entonces la incorporación de los valores negativos (pares e impares) sería aún mayor, por lo que se podría considerar a los menos infinito (−∞) y a los más infinito (+∞) como un conjunto de números infinitos más grande.
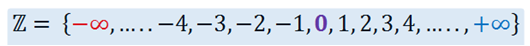
Mezclemos algo de Matemáticas sin secretos, pues sabemos de un valor trascendente muy usado en esta área de las ciencias y me refiero a


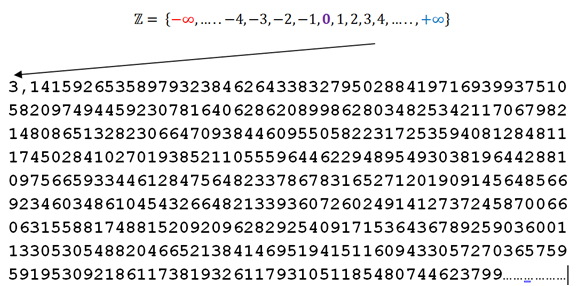
Espero que con estos ejemplos haya quedado clara la noción que tenemos de los números infinitos, con una ilimitada cantidad de dígitos, pero en algún momento debemos ver que no existe un infinito tan grande, ya que será superado por otro ∞ aún mayor.
Apoyo bibliográfico y fuente de imágenes
Nuestras ideas y conocimientos que podamos tener sobre el tema tratado en este artículo pueden ampliarse de manera voluntaria al consultar el siguiente catálogo de referencias:
- Imagen de geralt: Portada con el símbolo ∞
- Imagen gif: Mecanismo de Bernoulli
- Infinito de oro
- Imagen de aitoff: Número Pi
- Imagen de aitoff: Dígitos de Pi
- Nota de prensa: Nunca sabremos si el Universo es infinito
- Wikipedia: Universo
- Nota: Universo infinito
- Boletín: Concepto de infinito
- Nota Significado de infinito
y todos los conjuntos numéricos,
¿todavía no alcanzamos el INFINITO?
¡Felicidades! Esta publicación obtuvo upvote y fue compartido por @la-colmena, un proyecto de Curación Manual para la comunidad hispana de Hive que cuenta con el respaldo de @curie.
Si te gusta el trabajo que hacemos, te invitamos a darle tu voto a este comentario y a votar como testigo por Curie.
Si quieres saber más sobre nuestro proyecto, acompáñanos en Discord: La Colmena.
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Please consider using the STEMsocial app app and including @stemsocial as a beneficiary to get a stronger support.