Paolo Ruffini en la solución de polinomios

[ycam]

Polinomios y método de Ruffini

^{Factorización y División de Polinomios}

Los procedimientos matemáticos para la resolución de problemas que involucran a monomios, binomios o polinomios en general, suelen ser resueltos aplicando el Método o Regla de Ruffini en honor al matemático de origen italiano Paolo Ruffini. Confesaré que este tema fue uno de mis preferidos durante mis estudios de bachillerato y mis amigas me buscaban para que se los explicara con el libro de Matemáticas de Navarro, una bonita experiencia en mis tiempos de estudiante.

El libro texto de Navarro se llamaba: Curso propedeútico de Matemáticas y abarcaba varios temas desarrollados desde el primero al quinto año de bachillerato, por lo que se podía repasar cualquier detalle de operaciones básicas y tratar de resolver los problemas que se planteara cualquier temerario profesor.

Factorización:

Cuando queremos escribir un número de forma factorizada, debemos encontrar sus "factores primos" o números divisores que lo descomponen, y que al multiplicarlos nos da el número original. Veamos el siguiente ejemplo: En en caso de los polinomios resulta en hallar las raíces del polinomio para representarlo de forma abreviada, pero considerando el cociente y residuo como si se tratase de una división numérica.

La representación de un polinomio se inicia con la letra P seguida de la letra variable entre paréntesis, después del signo de igualdad y los factores del polinomio, comenzando con el de mayor grado hasta el término independiente.

En este caso, nuestro polinomio es de tercer grado, así que procedemos a hallar las posibles raíces enteras o fraccionarias que deben estar compuestas por los divisores del término independiente (TI) = −4 y/o del coeficiente que acompaña al término de mayor grado, en el caso de las raíces fraccionarias.

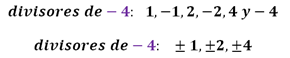
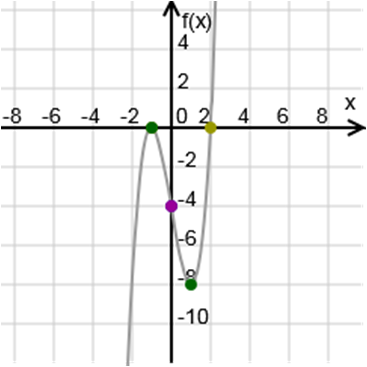
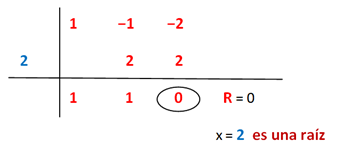
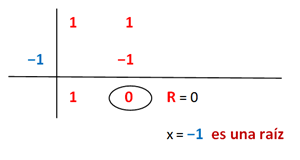
Raíces por tanteo:

para hallar las raíces de esta función polinómica debemos proceder con el tanteo, usando estos divisores de 4 hasta hacer que P(x) = 0.

Sólo 2 divisores de −4 hacen 0 al polinomio, por lo que nos indica que al graficar esta función vamos a observar que la curva intercepta con el eje de las abscisas en estos 2 puntos, x₁ = −1 y x₂ = 2

En algunas ocasiones es conveniente obtener el coeficiente 1 en el término de mayor grado, así nos libramos de las raíces fraccionarias, veamos el mismo ejemplo:

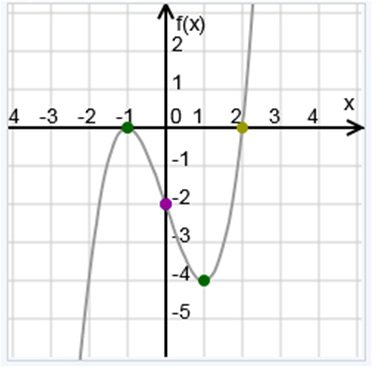
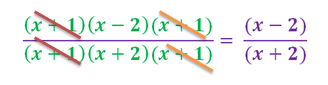
Cuando se desea factorizar un polinomio se utilizan estas raíces conformando varios binomios que al multiplicarlos nos resulta el polinomio a factorizar. En ocasiones resulta complicado hallar las raíces enteras de manera rápida y sencilla, por lo que se recurre al Método de Ruffini para obtener el divisor que haga 0 al residuo y por último multiplicar los binomios formados por estos divisores.

El procedimiento es sencillo, debemos ordenar los términos del polinomio por el de mayor grado y colocar los coeficientes que acompañan a la variable, si llegare a faltar se coloca un 0 en su lugar. Al lado izquierdo vamos a colocar cada uno de los divisores del TI y vamos multiplicando, sumando y restando cada término hasta obtener el último número igual a cero, esto es el residuo = 0, para que sea considerado como una raíz del polinomio. En el resultado de arriba es evidente que x = 1 no es raíz del polinomio P(x) = x³ − 3x − 2

En este punto podemos escribir la factorización del polinomio como, P(x) = x³ − 3x − 2 = (x + 1)(x² − x − 2)

En este punto podemos escribir la factorización del polinomio como, P(x) = x³ − 3x − 2 = (x + 1)(x + 1)(x − 2)

ya que el último resultado puede escribirse en forma aritmética como x - 2, o si lo prefieren seguir desarrollando por el Método de Ruffini:

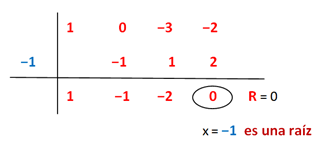
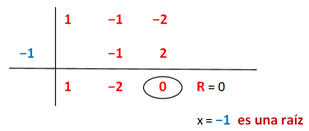
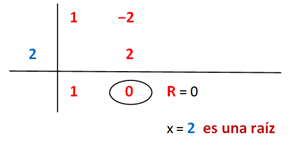
En el segundo paso pudimos seguir el procedimiento del tanteo y probar con el divisor +2 o −2 para ver si son raíces del subpolinomio (x² − x − 2)

luego, seguimos el Método de Ruffini Del mismo modo podemos escribir la factorización del polinomio como: P(x) = x³ − 3x − 2 = (x + 1)(x − 2)(x + 1), y como toda una buena ingeniera amante de la matemática puedo confirmar que el orden de los factores en esta multiplicación, no altera el producto.

Retomando el ejercicio planteado en la portada de este artículo, debemos dividir 2 polinomios:

sabiendo que el polinomio del numerador puede ser escrito de forma factorizada como:

y si mis queridos lectores realizan la tarea de resolver la forma factorizada del polinomio que ocupa el lugar del denominador, pues llegarán al siguiente resultado:

realizamos la división de polinomios P(x)/D(x), para obtener:

Este procedimiento de factorización es muy utilizado en ingeniería, física y matemáticas, no sólo a nivel de educación básica o secundaria, sino también en los estudios universitario y puedo decirles que facilita mucho la resolución de problemas en la carrera de Ingeniería.

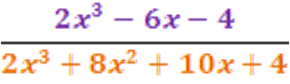
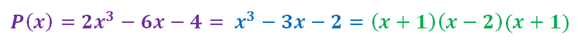
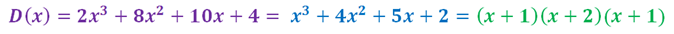
Apoyo bibliográfico y fuente de imágenes

Nuestras ideas y conocimientos que podamos tener sobre el tema tratado en este artículo pueden ampliarse de manera voluntaria al consultar el siguiente catálogo de referencias:

• Imagen de portada: Polinomios
• Blog: Regla de Ruffini
• Nota: La Regla de Ruffini para resolver problemas y factorizar
• Youtube: Método de Ruffini

Visita mi BLOG para ver temas interesantes sobre Matemáticas e Ingeniería

Comments

[acont]

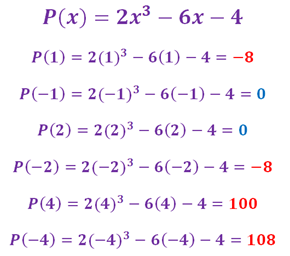
Método de Ruffini, recuerdo usar esto bastante en las clases de cálculo en la universidad y en bachillerato. Saludos!

[ycam]

Cálculo I en la universidad como repaso, pero en bachillerato fue un tema muy ameno para mi.
Gracias por tu comentario.

[steemstem]

Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!

Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).

Please consider using the STEMsocial app app and including @stemsocial as a beneficiary to get a stronger support. 
 

[edu-venezuela]

[edu-venezuela]