Expresiones algebraicas, desarrollo matemático

[ycam]

Expresiones Algebraicas

^{Tratamiento matemático de ecuaciones y polinomios}

Las operaciones aritméticas son muy comunes en todas las actividades de aprendizaje de las Matemáticas, por lo que se hace imprescindible el dominio de la suma, resta, multiplicación, división y hasta la potenciación junto a la radicación. También es importante saber discriminar las expresiones algebraicas y el planteamiento del problema para estar seguros de aplicar las reglas y procedimientos adecuados, por ejemplo en los casos siguientes:

ecuación de segundo grado: X² − 3X + 2 = 0 función cuadrática: f(X) = X² − 3X + 2 polinomio de grado 2: X² − 3X + 2

Repasaré con la ecuación de segundo grado, donde se deben hallar los valores de la variable X que cumplan con la igualdad (= 0), hallando las raíces:

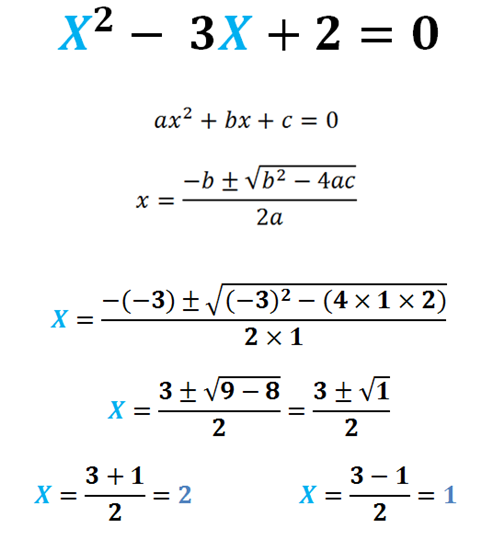
Un procedimiento sencillo, aplicando la fórmula cuadrática para resolver una ecuación cuadrática!

Por otro lado, recordemos que la función cuadrática, se puede analizar de forma gráfica o analítica asignando valores arbitrarios a la variable X y obteniendo los números de salida para conformar la imagen de esa función. No lo voy a desarrollar aquí, pero el Dominio: (−∞,∞), {x|x ∈ ℝ} muy amplio para valores positivos y negativos, además está definida para x = 0, donde el Rango: [−¼,∞), {y|y ≥ −¼}. Veamos la forma gráfica que tiene esta función:

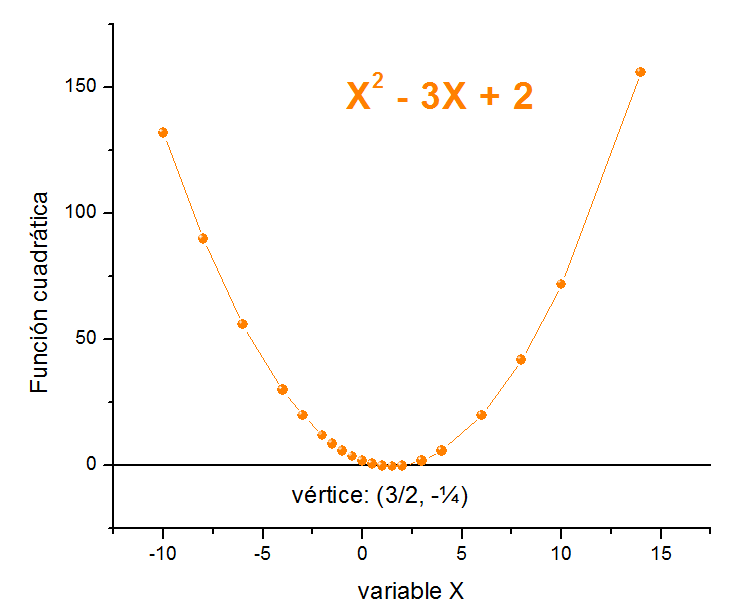
Polinomios

En el caso de una expresión algebraica donde se nos indique que se trata de un polinomio, una composición de coeficientes, variables y grados del polinomio y términos. En el siguiente gif trataré de representar cada uno de los componentes de un polinomio.

Para facilitar la comprensión de las operaciones aritméticas sobre los polinomios, trataremos 2 expresiones algebraicas de grado 2 y donde el término independiente es 0.

P(X) = 3X² + 2X Q(X) = 2X² + 4X

---

Operaciones con Polinomios

, es común realizar las operaciones aritméticas a este tipo de expresión algebraica: suma, resta, división y multiplicación hasta por un número real. Las metodologías se basan en operar miembros de grado idéntico, considerando los símbolos positivos y negativos, por ejemplo veamos la suma de P(X) + Q(X):

La suma de 2 polinomios con todos los términos del mismo signo, resulta en coeficientes incrementados y por ende la curva también aumenta debido a la contribución de cada polinomio.

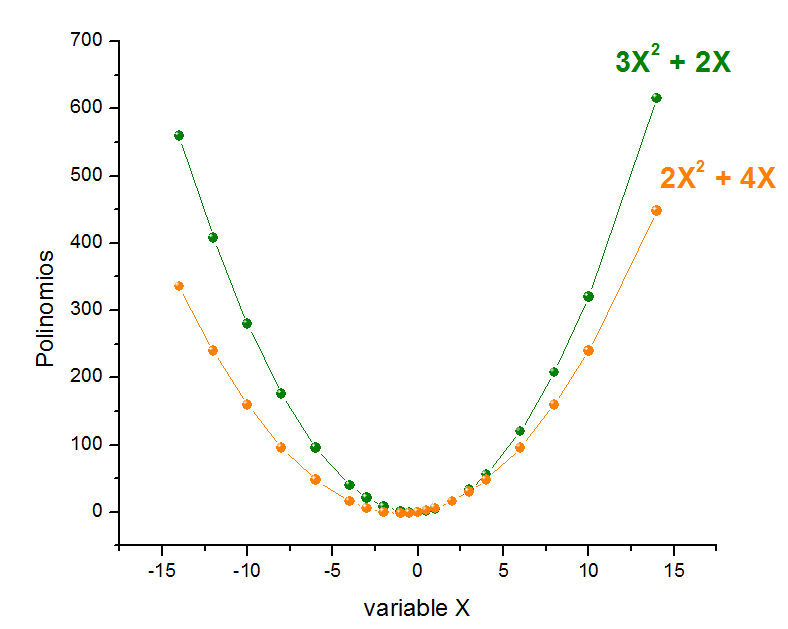
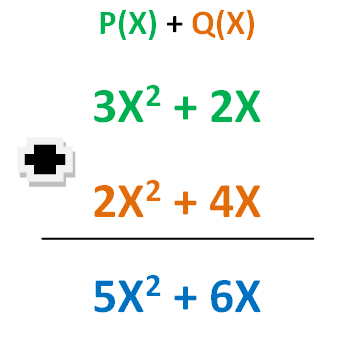
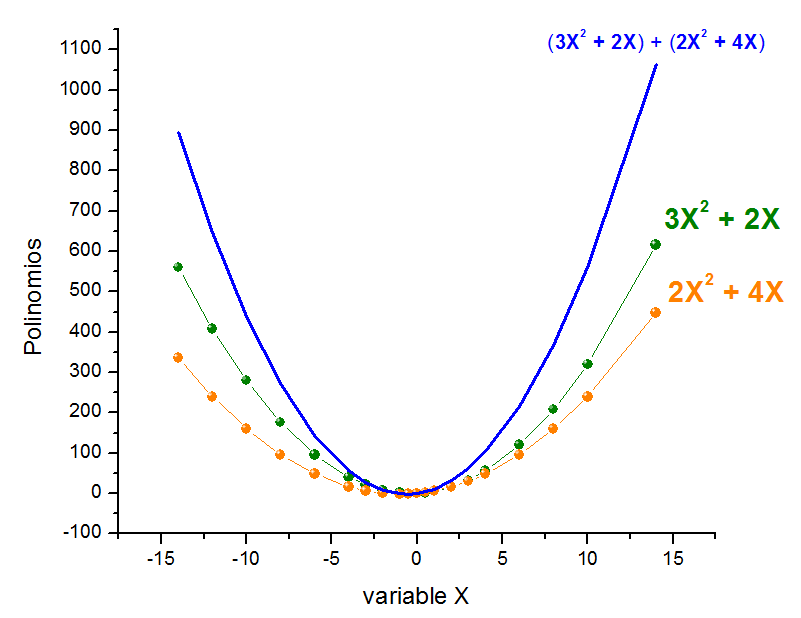
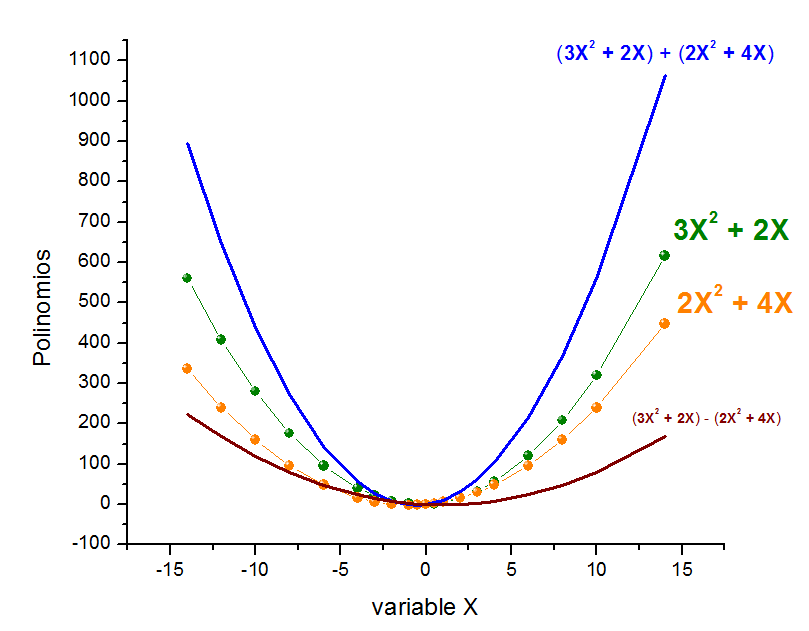
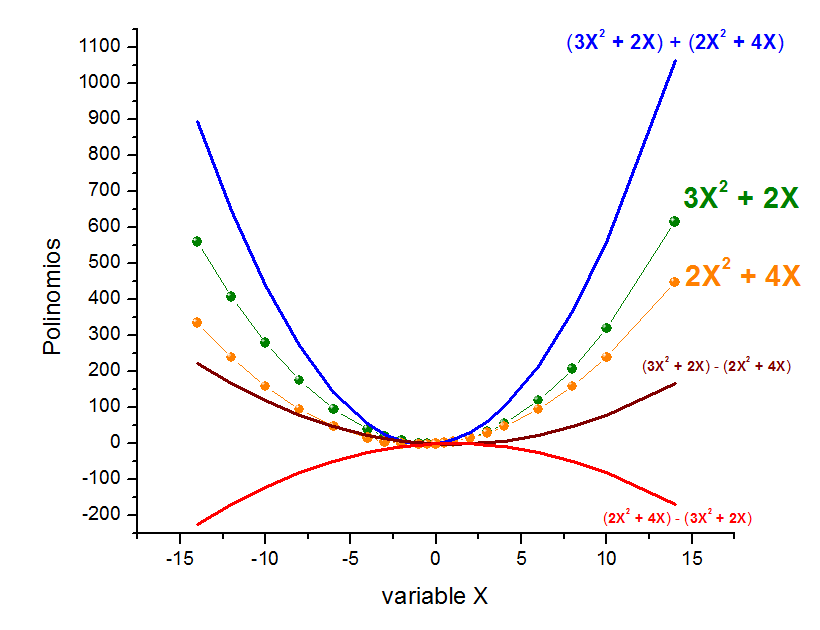
La forma de la curva, el foco, el vértice, la directriz y el eje de simetría de la gráfica de un polinomio, puede verse afectada debido a la contribución de otro polinomio.

Atención al dato de @ycam

, la clasificación de los polinomios es muy amplia y si queremos entender y aprender todos y cada uno de los puntos críticos de estas expresiones algebraicas, pues nos debemos adentrar en el mundo de los polinomios homogéneos, incompletos, iguales y hasta nulos, esto es P(X) = 0.

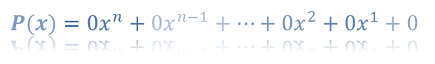
Apoyo bibliográfico y fuente de imágenes

Nuestras ideas y conocimientos que podamos tener sobre el tema tratado en este artículo pueden ampliarse de manera voluntaria al consultar el siguiente catálogo de referencias:

• Wikipedia: Polinomios
• Blog: Ecuaciones cuadráticas
• Blog: Suma de polinomios
• Imagen CC0: Imagen de la portada Math

¿Cualquier problema matemático tiene solución?
Comencemos con lo más básico,
con el planteamiento del problema!

Comments

[steemstem]

Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!

Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).

Please consider using the STEMsocial app app and including @stemsocial as a beneficiary to get a stronger support. 
 

[edu-venezuela]