
Repository
What will I learn
- Coverting points to coordinate tuples
- Finding the outer bounds of the grid
- Calculating the distance between two locations
- Calculating sum of distances to all locations
Requirements
- Python 3.7.2
- Pipenv
- git
Difficulty
- basic
Tutorial
Preface
This tutorial is part of a course where solutions to puzzles from Advent of Code 2018 are discussed to explain programming techniques using Python. Each puzzle contains two parts and comes with user specific inputs. It is recommended to try out the puzzle first before going over the tutorial. Puzzles are a great and fun way to learn about programming.
While the puzzles start of relatively easy and get more difficult over time. Basic programming understanding is required. Such as the different type of variables, lists, dicts, functions and loops etc. A course like Learn Python2 from Codeacademy should be sufficient. Even though the course is for Python two, while Python 3 is used.
This tutorial will look at puzzle 6
The code for this tutorial can be found on Github!
Puzzle 6
The puzzle is about calculating distances between coordinates in an infinite grid.
Part one
A list of coordinates is given which describe locations in a grid. Points in the grid that are closest to these locations belong to that specific location. Points that are equally far from multiple locations are denoted by .. Locations are denominated in capital characters while the points belonging to these location are denoted in smaller case characters.
aaaaa.cccc
aAaaa.cccc
aaaddecccc
aadddeccCc
..dDdeeccc
bb.deEeecc
bBb.eeee..
bbb.eeefff
bbb.eeffff
bbb.ffffFf
The questions for the first part of the puzzle is:
What is the size of the largest area that isn't infinite?
Points alongside the edges expand infinitely. So only locations that are enclosed by other locations have a non infinite size.
Coverting points to coordinate tuples
The input for the puzzle comes as a list of points that are separated by a ,.
181, 47
337, 53
331, 40
137, 57
200, 96
Reading these from the file, extracting the digits, converting them to digits and creating tuples can be done with a list comprehension.
# parse lines into (x, y) tuples
with open('input.txt', 'r') as file:
points = [tuple(map(int, re.findall(r'\d+', x))) for x in file]
This code is equivalent to:
locations = []
for line in file:
// extract digits
digits = re.findall(r'\d+', line)
// convert to int inside tuple
location = tuple(map(int, digits))
locations.append(location)
Where re.findall(r'\d+', line) extracts all the digits, map() applies int() to each value extracted and tuple() convert the list to a set.
Finding the outer bounds of the grid
While the grid is infinite in size the locations are in a finite grid. Calculating the borders of this grid can be done by looking for the min and max values of both the x and y coordinates.
# find the min / max bounds of all locations
x0, x1 = min(x for x, y in locations), max(x for x, y in locations)
y0, y1 = min(y for x, y in locations), max(y for x, y in locations)
Calculating the distance between two locations
To calculate the distance between two locations the Manhattan distance is given.
# manhattan distance
def distance(x1, y1, x2, y2):
return abs(x1 - x2) + abs(y1 - y2)
With the finite grid the distance to each locations from each point inside the grid can be calculated. Each location that has a infinite size has to be discarded. Points that are alongside the borders can be assumed to extend infinitely, the location that they belong to will be discarded.
counts = defaultdict(int)
infinite = set()
The results are stored inside counts while infinite locations are stored inside infinite.
# loop over each point in the finite grid
for y in range(y0, y1 + 1):
for x in range(x0, x1 + 1):
# find the distance to each location. Sort result by distance.
ds = sorted((distance(x, y, px, py), i) for i, (px, py) in enumerate(locations))
# when the first and second result are not the same there is no tie
# and the point belongs to a location.
if ds[0][0] != ds[1][0]:
counts[ds[0][1]] += 1
# points along the border are part of an infinite location
if x == x0 or y == y0 or x == x1 or y == y1:
infinite.add(ds[0][1])
# discard all infinite locations
for k in infinite:
counts.pop(k)
for i, (px, py) in enumerate(points) extracts the coordinates of each location and enumerates the location as i. This number is then used to refer back to the location. (distance(x, y, px, py), i) then calcuclates the distance to each location and stores this inside a tuple. sorted then sorts all the tuples by their first value, which is the distance.
if ds[0][0] != ds[1][0] Looks at the distance from the first and second tuple. When they are not equal there is no tie and the size of the area that it is closest to get increased by 1 counts[ds[0][1]] += 1
Points along the border are part of an infinite region and get discarded.
return max(counts.values())
Returns the maximum value sorted by the values of the dict.

Part two
What is the size of the region containing all locations which have a total distance to all given coordinates of less than 10000?
The second part of the puzzle is relatively easy. Instead of sorting for the shortest distance take the sum of all distances and check if this value is smaller than 10000 is sufficient.
Calculating sum of distances to all locations
counter = 0
# loop over each point in the finite grid
for y in range(y0, y1 + 1):
for x in range(x0, x1 + 1):
# calculate distances to each locations and sum all the values
# if the total value is smaller than 10000 add 1 to the counter
if sum(distance(x, y, px, py) for px, py in locations) < 10000:
counter += 1
sum(distance(x, y, px, py) for px, py in points) takes the coordinates for each location and calculates the distance from the point to each location. These values are then added together with sum().

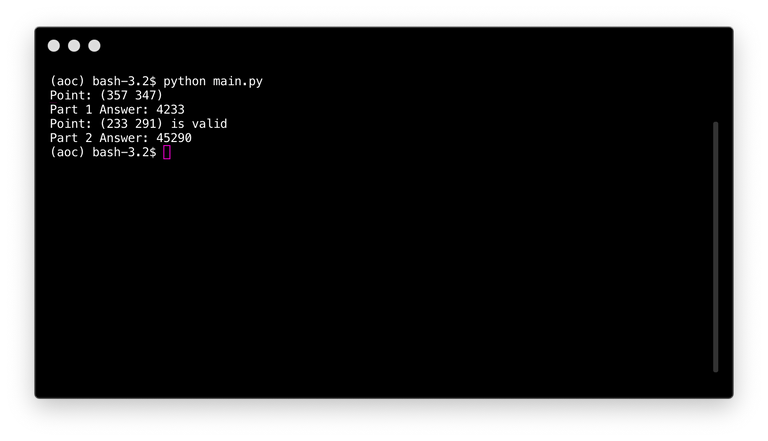
Running the code
Run the code with: python main.py. This returns both answers for the first and second part of the puzzle.
if __name__ == "__main__":
# read input file and convert to string
with open('input.txt', 'r') as file:
string = str([x.strip() for x in file][0])
print(f'Part 1 Answer: {part_1(string)}')
print(f'Part 2 Answer: {part_2(string)}')
Curriculum
Part 1, Part 2, Part 3, Part 4, Part 5
The code for this tutorial can be found on Github!
This tutorial was written by @juliank.
Thank you for your contribution @steempytutorials.
After reviewing your tutorial we suggest the following points listed below:
Excellent tutorial as you have accustomed us. The contribution is well explained and structured.
Using GIFs to show results is definitely better than standard still images.
We are waiting for more tutorials.Good Job!
Your contribution has been evaluated according to Utopian policies and guidelines, as well as a predefined set of questions pertaining to the category.
To view those questions and the relevant answers related to your post, click here.
Need help? Chat with us on Discord.
[utopian-moderator]
Thank you for your review, @portugalcoin! Keep up the good work!
Hi @steempytutorials!
Your post was upvoted by @steem-ua, new Steem dApp, using UserAuthority for algorithmic post curation!
Your post is eligible for our upvote, thanks to our collaboration with @utopian-io!
Feel free to join our @steem-ua Discord server
Hey, @steempytutorials!
Thanks for contributing on Utopian.
We’re already looking forward to your next contribution!
Get higher incentives and support Utopian.io!
Simply set @utopian.pay as a 5% (or higher) payout beneficiary on your contribution post (via SteemPlus or Steeditor).
Want to chat? Join us on Discord https://discord.gg/h52nFrV.
Vote for Utopian Witness!
Hi, @steempytutorials!
You just got a 1.02% upvote from SteemPlus!
To get higher upvotes, earn more SteemPlus Points (SPP). On your Steemit wallet, check your SPP balance and click on "How to earn SPP?" to find out all the ways to earn.
If you're not using SteemPlus yet, please check our last posts in here to see the many ways in which SteemPlus can improve your Steem experience on Steemit and Busy.