(Con éste, vamos por tres posts en esta secuencia. El anterior está en este enlace. A quienes son nuevos en el manejo de blogs les aclaro que los textos en azul son enlaces que los llevan a otras páginas.)
En mi país -Venezuela- la palabra coscorrón va con la segunda acepción que le da el DRAE: ese doloroso golpe en la cabeza producido con el nudillo saliente del dedo medio. Durante mucho tiempo el coscorrón fue un instrumento educativo al alcance de todos los padres y maestros; hoy es algo peligroso su intento. Una de las enseñanzas preferidas para la aplicación de esta técnica didáctica fue sin duda la tabla de multiplicar. Es mucho el ciudadano de hoy entrado en algunos añitos que recuerda el "4x3, 12", como la interrupción dolorosa del recitado "4x1, 4; 4x2, 8; 4x3, 11...". No se hacía esperar el coscorrón y la consiguiente imprecación: "4x3, 12... ¡bruto!".
Hoy los niños la tienen más fácil sin el coscorrón, pero la lata de repetir los recitados de las tablas sigue igualita.Se eliminó la parte física del tormento, pero la psicológica permanece intacta. A pocos maestros se les ocurre que a los niños les gusta jugar y que cosas como contar a saltos pudieran ser divertidas si nos ponemos a ello. Contar de 1 en 1 desde 1, da los múltiplos de 1; contar de 2 en 2 desde 2, da los múltiplos de 2; de 3 en 3 desde 3, los múltiplos de 3; etc. Pero eso es un jueguito que se puede hacer rellenando una tabla, como la de la izquierda de la foto que sigue, hasta llegar a la de la derecha:
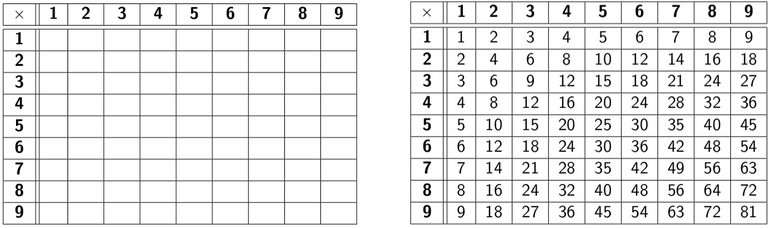
¿De cuántas maneras se puede convertir esta actividad en un juego? No sé. ¡Invente usted! Puede poner a Pedro y a Juan a competir por una línea, puede usted "competir" con ellos, puede jugarse a quién recuerda mejor una entrada en particular (4x3, 12, por ejemplo)... ¡qué sé yo! Pero la tabla pitagórica (así se llama el jueguito) pudiera ser un instrumento menos tortuoso que la repetición vacía de las benditas tablas de las contraportadas de los cuadernos. (Solo por proponer algo: se pueden inventar otras cosas.)
Jugando este juego con mi nieto de tercer grado, recibí una gran alegría cuando me hizo observar (con sus propias palabras, por supuesto) que la tabla era simétrica respecto a su diagonal. En otras palabras: que el orden de los factores no altera el producto. A diferencia de Manolito, mi nieto pudo ver esto sin conocerlo por vox populi. Pero la multiplicación tiene otras propiedades.
Una muy interesante es que se distribuye dentro de los términos de una suma. ¿Cómo es eso? Pongamos un ejemplo. Queremos multiplicar el resultado de 5+4 por 7. Entonces podemos hacer 5x7=35, 4x7=28, 35+28=63 o, con algo más de orden:
(5+4)x7 = 5x7 + 4x7 = 35 + 28 = 63
"¡Bah! ¿No es más fácil hacer simplemente 9x7=63?", me preguntará alguien de mentalidad práctica. Le responderé que sí, por supuesto. Pero la propiedad distributiva, que es como se llama este asunto, es la clave para entender por qué multiplicamos de la manera que multiplicamos cuando lo hacemos a mano. Por ejemplo, si vamos a multiplicar 34x2, tenemos que recordar que los números están escritos en sistema posicional decimal, así que 34 = 3 d + 4 u. Pero para la multiplicación es más facil escribir eso mismo como 34 = 30 + 4. ¿Por qué? Porque multiplicar por 10, o por 100, o por 1000, etc. es solo añadir ceros a la derecha del número. Eso se llama multiplicación por la unidad seguida de ceros.
34x2 = (30 + 4)x2 = 30x2 + 4x2 = 60 + 8 = 68
Pero la multiplicación anterior es muy fácil, porque no hay que llevar. Probemos entonces con 49x7:
a) 49x7 = (40 + 9)x7 = 40x7 + 9x7
b) 9x7 = 63 = 6 d + 3 u. Tomamos nota de las unidades y dejamos pendientes (llevamos) las 6 d.
c) 40x7 = 280 = 2 c + 8 d. Del paso anterior llevamos 6 d, que sumadas a las 8, resultan 14 d = 1 c, 4 d. Total parcial: 3 c + 4d. El total general es, entonces, 3 c, 4 d, 3u. Pero todo se escribe así:
El último caso por ver es el de ambos factores con más de una cifra. En este caso se utiliza la propiedad distributiva dos veces. ¿Cómo? Bueno... avanti. Pongamos que queremos multiplicar 43x27. Pensada en sistema posicional decimal, la cosa queda así:
43x27 = (40 + 3)x(20 + 7)
y entonces los pasos son los siguientes:
a) Distribuyo las 7 u del segundo factor con el primer factor: (40 + 3)x7 = 40x7 + 3x7 = 280 + 21 = 301.
b) Distribuyo las 2 d del segundo factor con el primero: (40 + 3)x20 = 40x20 + 3x20 = 800 + 60 = 860.
c) Sumo ahora las partes a) y b) 301+860 = 1161.
Eso se puede distribuir así:
Finalizo este post con una reflexión. Whitehead dijo que la humanidad avanza aumentando el número de cosas que pueden hacerse mecánicamente, sin pensar en ellas. Nadie maneja un carro pensando, cuando pisa el acelerador en la inyección de gasolina, la consiguiente explosión, etc. Pero si lo siento temblando ante la pisada del acelerador debo pensar que hay un problema con este proceso. La matemática es odiada porque hay muchas cosas que se hacen en ella sin motivación aparente. Lo dije y lo repito ahora: en los prestidigitadores creemos, pero sabemos que nos están engañando. Cuando aprendemos, no nos gustan estos engaños: es mejor ver de dónde salen las cartas.
Fe de errata. En el enlace anterior sobre la resta cometí un error imperdonable, que me lo hizo ver el querido amigo Walter Beyer: confundí los papeles de minuendo y sustraendo. Por supuesto que ya está editada y corregida la entrada, pero no podía pasar por alto el detalle.

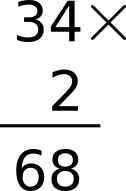
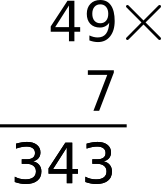
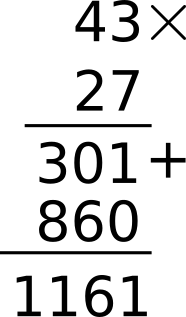
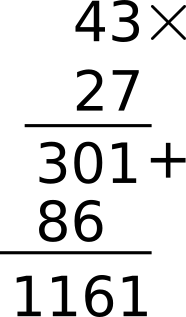
Gracias por seguir alegrándonos la lectura con tus publicaciones.
Un abrazo.
Gracias a ti por el estímulo.
Hola. Por casualidad me tope con tu perfil. Y te invito a que visites la etiqueta #steem-espanol. Es una comunidad científica de habla hispana que seguramente apoyará tus post debido a que escribes matemática de una forma distinta.