Die Corona-Krise und der damit verbundene Lockdown haben große Teile der Welt in arge Bedrängnis gebracht. Nach wie vor ist fraglich, ob die verhängten Maßnahmen tatsächlich gerechtfertigt waren. Besonders im Fokus steht hier der für die Diagnose des Virus verwendete PCR‑Test. Oft werden beeindruckende Zahlen bezüglich der Verlässlichkeit von Corona-Tests angegeben, teilweise weit über 99 % [1]. Dennoch darf niemals die Häufigkeit einer Erkrankung in Bezug auf die Gesamtbevölkerung vergessen werden. Mit dem „Satz von Bayes“ kann unter Verwendung der Gesamtzahl von Erkrankten und den Kennzahlen des PCR-Tests abgeschätzt werden, wie groß die Zuverlässigkeit von solchen Tests wirklich ist [2,3]. In diesem Artikel wollen wir zunächst die aktuellen Daten der Corona-Krise unter Berücksichtigung der „Bayes-Statistik“ analysieren. Im zweiten Teil soll geprüft werden, inwiefern Korrelationen von Corona-Daten in Bezug auf Altersstruktur, Entwicklungsniveau, Bevölkerungsdichte, Wohlstand etc. bestehen. Am Ende gehen wir auf Maßnahmen ein, die jeder treffen kann, um seine Gesundheit bestmöglich zu fördern. Außerdem wollen wir überlegen, ob die Krise schon vorbei ist oder gerade erst begonnen hat.
Der Satz von Bayes & Corona-Tests
Der Satz des berühmten Mönches und Mathematikers Reverend Thomas Bayes (vermutlich 1701 bis 1761) bietet eine Möglichkeit Wahrscheinlichkeiten unter Berücksichtigung von Vorwissen zu ermitteln.

Abbildung 1 Neben Gauß wohl einer der bedeutensten Statistiker: Reverend Thomas Bayes. Ob das Bild tatsächlich ihn zeigt ist umstritten 😉. By Wikipedia. Public Domain. No copyright.
Diese Art der Statistik wird nicht nur von unserem Gehirn verwendet, um die vermeintliche Realität zu konstruieren [4]. Sie hat tatsächlich viele Anwendungsfälle [2–5]:
- Lotterien: Wie hoch ist Wahrscheinlichkeit, dass x Prozent aller Lose gewinnt, wenn bereits y Lose gewonnen haben.
- Katastrophenmanagement: Wie hoch ist die Wahrscheinlichkeit Vermisste an einem Ort zu finden, wenn die Suche an anderen Orten bereits erfolglos war.
- Unplausible Resultate durchschauen: 100 Männer haben eine Durchschnittsgröße von 210 cm, der Abgleich mit anderen Daten (Vorwissen!) lässt eine Korrektur zu.
Der Satz ist folgendermaßen definiert:
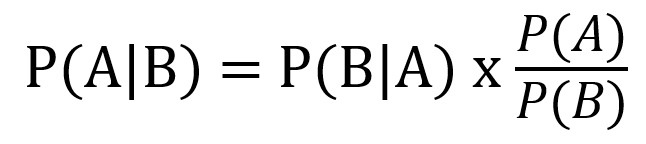
A wäre in dem Fall der Anteil positiver Tests und B der Anteil des Auftretens tatsächlicher Erkrankungen.
A: Test ist positiv, d.h. +
B: Patient ist tatsächlich krank, d.h. D = 1 (D steht für „Disease“)
Die Wahrscheinlichkeit, dass ein Patient tatsächlich krank und die Diagnose gleichzeitig positiv ist, wird auch als Sensitivität bezeichnet. Oder anders ausgedrückt der Anteil positiver Testergebnisse unter Kranken [2].
Die Spezifität hingegen ist, die Wahrscheinlichkeit, dass ein Patient nicht krank ist und ich auch tatsächlich keine Krankheit diagnostizieren kann, beziehungsweise der Anteil negativer Testergebnisse unter Gesunden [2].
Im Falle von Corona (ich verwende diesen Begriff hier für COVID-19 bzw. SARS-CoV-2) gehen wir von einer Spezifität und Sensitivität von 99% aus. Das heißt sollte ich im Labor den PCR-Test validieren und ein Ergebnis von 100 Tests positiv sein, obwohl ich statt dem Corona‑Virus einen anderen Erreger überprüft habe, dann habe ich eine Spezifität von 99% (1 in 100 hat versagt). Hingegen werde ich bei 99% Sensitivität nur einmal den Corona-Virus nicht detektiert haben, obwohl ich nur diesen Untersucht hatte (99 von 100 haben funktioniert). Nun gilt es noch die Gesamtbevölkerung miteinzubeziehen, in Deutschland sind dies 83803229 oder rund 84 Millionen Menschen. Insgesamt wurden 7418812 (oder rund 7,4 Millionen) Menschen überprüft, dies sind etwa 8,85% der Gesamtbevölkerung. Davon wurden 206741 (also rund 0,2 Millionen) Personen als Corona-positiv bewertet. Dies sind etwa 0,247% der Gesamtbevölkerung. 99,753% der Bevölkerung waren demnach „gesund“ (Stand 27.07.2020 vormittags).
Wir setzen nun alles nach und nach in den Satz von Bayes ein:
P(B|A) = Die Wahrscheinlichkeit, dass positiv getestet wurde und gleichzeitig auch eine Erkrankung vorlag
= Sensitivität
= Pr(+|D=1)
= 0,99
P(A) = Anteil der Erkrankung in der Bevölkerung = Pr(D=1) = 0,247/100 = 0,00247.
P(B) = Anteil tatsächlich positiv getesteter Personen in der Bevölkerung
= Sensitivität x Anteil Erkrankung in Bevölkerung + Anteil unspezifisch-getesteter Personen x Anteil Gesunder
= Pr(+|D=1) * Pr(D=1) + Pr(+|D=0) * Pr(D=0)
(Anmerkung: Pr(+|D=0) ist in dem Falle = 1 – Spezifität, weil positiv getestet wurde, aber die Person nicht krank ist)
Den Satz von Bayes kann man demnach in Bezug auf Corona-Tests auch so schreiben:
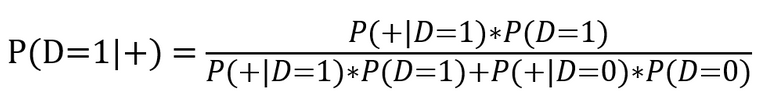
Eingesetzt in den Satz von Bayes ergibt sich somit für Deutschland:
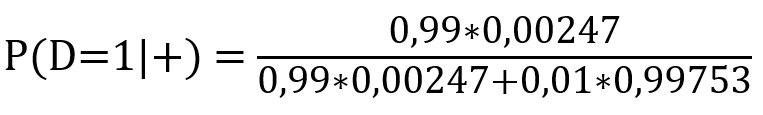
Wenn alles richtig eingesetzt und ausgerechnet wurde, ergibt sich ein Wert von rund 0,197. Demnach liegt die Wahrscheinlichkeit, dass ein positiver Test auch tatsächlich eine Corona-Erkrankung anzeigt in Deutschland gegenwärtig (Stand 27.07.2020 vormittags) bei etwa 19,7%. Es ist somit davon auszugehen, dass über 80% der Tests in Deutschland falsch-positiv waren. Corona also diagnostiziert wurde, aber in Wahrheit keine Corona-Erkrankung vorlag.
Konsequenz der Bayes-Statistik für die Bewertung der Pandemie
Wie bereits oben erwähnt ist die Bayes-Statistik dafür geeignet unplausible Ergebnisse zu korrigieren. Wie oben errechnet ist allein in Deutschland davon auszugehen, dass ca. 80% falsch-positiv sind. Tatsächlich wurde vereinzelt berichtet, dass in Abhängigkeit vom Untersuchungsort teilweise mehr als 80% entweder milde oder gar keine Symptome zeigten [6]. Wir schauen uns aus diesem Grunde die Corona-Fälle, sowie Todesfälle an, welche offiziell (nicht Bayes-korrigiert) und Bayes-korrigiert errechnet werden können (Abbildung 1).
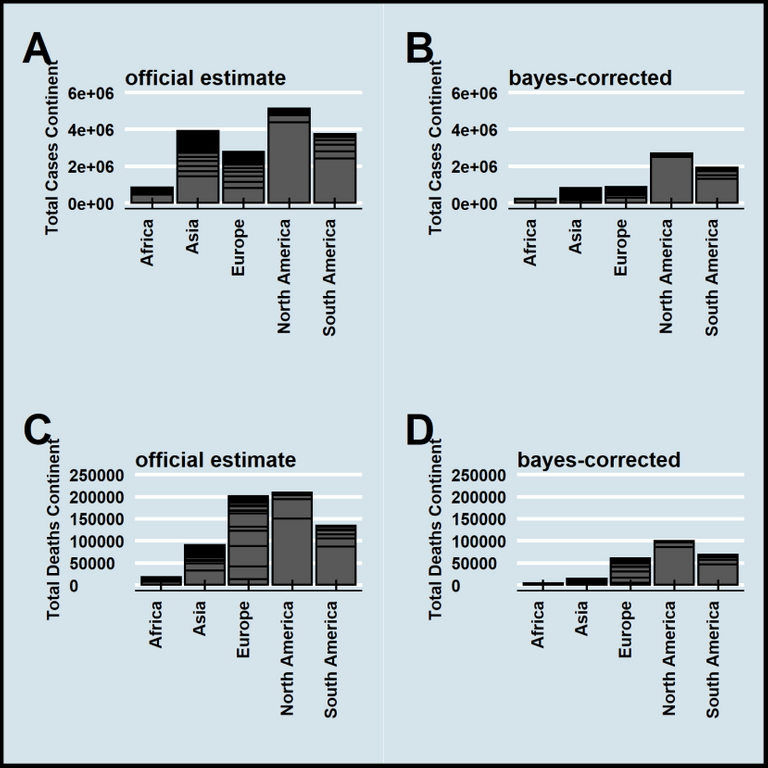
Abbildung 2 Corona-Tote nach Kontinent. „official estimate“ = offizielle Zahlen. „bayes-corrected“ = korrigierte Zahlen anhand des „Satzes von Bayes“. Insgesamt flossen die Daten von 188 Staaten in die Analyse ein. Australien und Ozeanien wurden entfernt, da nicht genug Werte zusammenkamen. Stand 27.07.2020. Made by Chapper – unrestricted use allowed.
In Abbildung 2 ist zu erkennen, dass die meisten Corona-Fälle in Nordamerika, Asien, Südamerika und Europa aufgetreten sind (Abbildung 2A). Nach Berücksichtigung falsch-positiver Resultate bilden Nord- und Südamerika die kritischsten Erdteile (Abbildung 2B). In Bezug auf Sterbefälle liegen Nordamerika und Europa an erster Stelle (Abbildung 2C). Die Korrektur führt dazu, dass Nordamerika der Kontinent mit den meisten Sterbefällen ist (Abbildung 2D). Interessant ist vor allem der starke Abfall an Zahlen in Asien nach Korrektur. Zusammengenommen wären daher weltweit „nur“ etwa 6,5 Millionen Menschen statt 16,4 Millionen Menschen an Corona erkrankt und statt 0,65 Millionen Menschen wären in etwa 0,245 Millionen Menschen an Corona gestorben.
Fraglich ist nun selbstverständlich was man tun kann, um den Anteil falsch-positiver Resultate zu verringern. Nur so kann eine klare Einschätzung der Lage vorgenommen werden. Natürlich käme eine Verbesserung der PCR-Tests in Betracht, wobei 99% Spezifität und Sensitivität schon sehr gut sind. Eine Erhöhung von 99% auf 99,9% würde den Anteil falsch-positiver Ergebnisse in Deutschland beispielsweise lediglich von etwa 80,3% auf 80,2% senken. Das heißt an den Tests kann man nur noch sehr wenig ändern. Eine andere Möglichkeit bestünde in der Erhöhung der Menge an Tests. Wir wollen aus diesem Grunde die Korrelation zwischen „Wahrscheinlichkeit richtig-positiver Ergebnisse“ und der „Gesamt-Testmenge in Prozent“ beziehungsweise der „Gesamt-Fallzahl“ überprüfen (Abbildung 3).
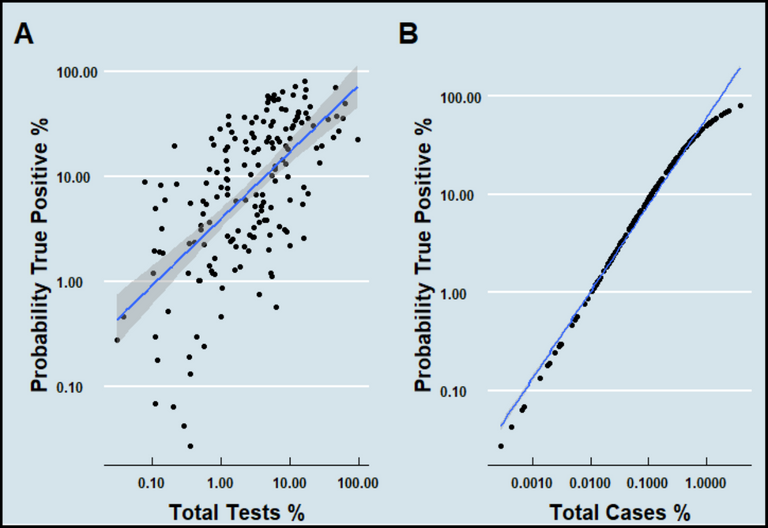
Abbildung 3 Korrelation der „Gesamtzahl an Tests in Prozent“ („Total Tests %“) (A) und „Gesamtzahl an Corona-Fällen in Prozent“ („Total Cases %“) (B) zur „Wahrscheinlichkeit eines richtig-positiven Ergebnisses“ („Probability True Positive %“). Korrelationskoeffizient (R2) in A = 0,627 und in B ≈ 1 (Methode: Spearman). Alle Länder mit Fallzahlen oder Testzahlen unter 0,001% wurden aus der Analyse entfernt. Sowohl die x- als auch y-Achse sind in log10 angegeben. Insgesamt flossen nur die Daten von 176 Staaten in die Analyse ein. Stand 27.07.2020. Made by Chapper – unrestricted use allowed.
Anhand von Abbildung 3 ist erkennbar, dass lediglich das Vorhandensein tatsächlicher Erkrankungen den Fehler in der Messung entscheidend senken kann. Die Korrelation höher Testanzahl zur „Wahrscheinlichkeit richtig-positiver Ergebnisse“ beträgt etwa 0,627, d.h. die Korrelation ist relativ schwach. Demgegenüber steht ein Korrelationskoeffizient (R2) von rund 1,0 im Falle tatsächlich hohen „Fallzahlen“ zur „Wahrscheinlichkeit eines richtig-positiven Ergebnisse“. Daraus folgt, dass vor allem Tests in konkreten Verdachtsfällen vorzunehmen sind. Abbildung 4 zeigt einen Überblick über die weltweite Situation.
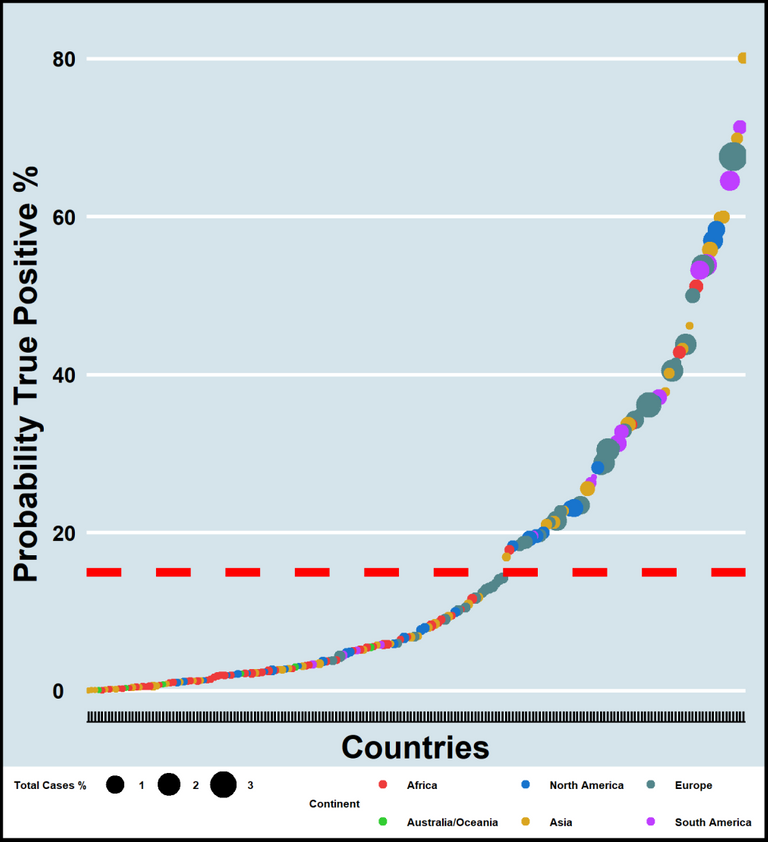
Abbildung 4 Länder der Erde in denen Corona-Erkrankungen registriert wurden. Gezeigt ist die „Wahrscheinlichkeit richtig‑positiver Ergebnisse“, sowie die relative Sterberate (Größe der Punkte). Die rote Linie zeigt den „Cutoff“ von etwa 15%. Insgesamt flossen die Daten von 194 Staaten in die Analyse ein. Stand 27.07.2020. Made by Chapper – unrestricted use allowed.
In Abbildung 4 ist zu sehen, dass eine große Mehrheit von Staaten einen geringen Anteil vermeintlich richtig-positiver Ergebnisse aufweist ("Probability True Positive %"<15%). Nur 71 von 194 Staaten zeigen eine „Wahrscheinlich für ein richtig-positives Ergebnis“ von ≥15%. Staaten mit einer geringen „Wahrscheinlichkeit für ein richtig-positives Ergebnis“ befinden sich vor allem in Afrika, Asien, manchen lateinamerikanischen Staaten, aber auch in Europa.
Bei Ländern mit den verlässlichsten Zahlen in Bezug auf „Wahrscheinlichkeit eines richtig-positiven Ergebnisses“ handelt es sich vor allem um Kleinstaaten, um Staaten des Mittleren Ostens (insbesondere Golfstaaten), sowie um süd- und nordamerikanische Staaten (Tabelle1).
Tabelle 1 Top15-Staaten nach „Wahrscheinlichkeit für richtig-positives Ergebnisse“ (A, Probability), „Anzahl Corona-Fälle in %“ (B, Caserate), sowie „Anzahl an Corona-Fällen in % korrigiert“ (C, Caserate_corr). Stand 27.07.2020. Made by Chapper – unrestricted use allowed.
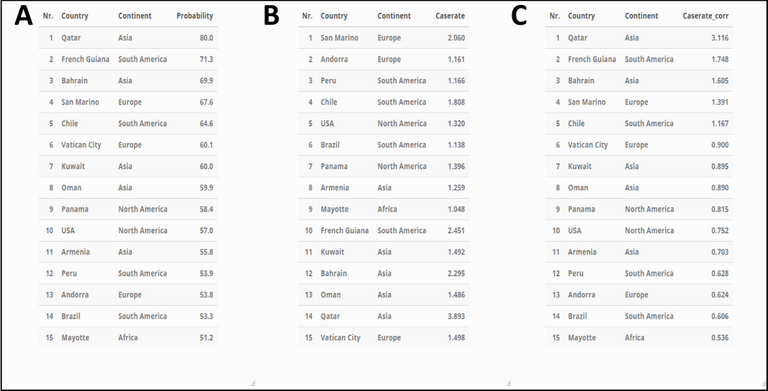
In den Top15 kommen somit nur drei europäische Länder vor, diese sind ausnahmslos Kleinstaaten (San Marino, Vatikan und Andorra). Weiterhin fällt auf, dass nur ein Industriestaat in den Top15 vorhanden ist, nämlich die USA. Die Reihenfolge ändert sich ein wenig, wenn man die Top15 der Staaten gemäß „Corona-Fällen in %“ betrachtet (Tabelle 1B). Unter Verwendung der errechneten „Wahrscheinlichkeit eines richtig-positiven Ergebnisses“ finden wir jedoch die Reihenfolge aus Tabelle 1A wieder (Tabelle 1C). Interessanterweise sind in der Betrachtung der höchsten Todesraten vor allem europäische Länder vorhanden (Tabelle 2).
Tabelle 2 Top15-Staaten nach „Wahrscheinlichkeit für richtig-positives Ergebnisse“ (A, Probability), „Anzahl Todesfälle in %“ (B, Deathrate), sowie „Anzahl an Todesfällen in % korrigiert“ (C, Deathrate_corr). Stand 27.07.2020. Made by Chapper – unrestricted use allowed.
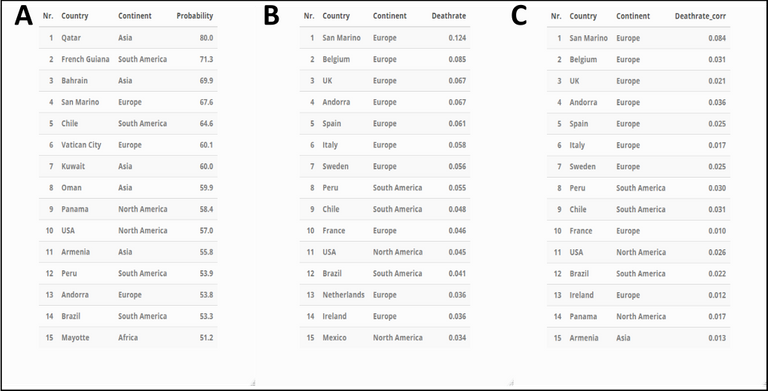
Tabelle 2 zeigt deutlich, dass anhand der offiziellen Zahlen vor allem europäische Länder eine enorm hohe Sterberate ausweisen. Außerdem vertreten sind süd- und nordamerikanische Staaten. Dieser Zustand ändert sich auch nach Korrektur unwesentlich (vergleich Tabelle 2 B & C).
Zusammenfassung
Weltweit ist davon auszugehen, dass rund 40% der Corona-Fälle und Corona-Toten auch "korrekt" diagnostiziert wurden. Eine Erhöhung der Testhäufigkeit würde dieses Ergebnis nicht verbessern. Wichtig ist die Prädiagnostik. In Deutschland muss davon ausgegangen werden, dass etwa 20% aller Fälle "richtig" diagnostiziert wurden. Die genauste Diagnostik wurde vor allem in Kleinstaaten und Golfstaaten vorgenommen. Dennoch weisen auch nach Korrektur europäische Staaten (San Marino, Belgien, UK, Andorra, Spanien, Italien, Schweden…) die höchsten Sterberaten auf.
Wir wollen in der Folge untersuchen, woher diese Unterschiede rühren.
Fortsetzung folgt im zweiten Teil…
Daten & Methoden
Die verwendeten Staaten stammen von der Website https://www.worldometers.info/coronavirus/ und wurden mittels Webscraping in R & RStudio (Version 3.6.3) geladen:
R Core Team (2020). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. URL https://www.R-project.org/.
Folgende Packages habe ich zur Auswertung verwendet:
tidyverse, rvest, plyr, table1, corrplot, Hmisc, ggthemes, broom, ggrepel, ggpubr, factoextra, rstatix, gridExtra, scales, psych, kableExtra, knitr
Den Code stelle ich euch auf Anfrage gern zur Verfügung.
Literatur
[1] Mitteldeutsche Zeitung, Wie sicher sind Corona-Tests? https://www.mz-web.de/leben/wie-sicher-sind-corona-tests--36644226.
[2] Jürgen Heddrich & Lothar Sachs, Angewandte Statistik: Methodensammlung mit R, sixteenth ed., Springer Spektrum.
[3] Marc Dressler, Spektrum der Wissenschaft.
[4] Anil K. Seth, Spektrum der Wissenschaft.
[5] Dominik R. Bach, Spektrum der Wissenschaft.
Posted from my blog with SteemPress : http://worldofchapper.de/rp295320-ovh/index.php/2020/07/27/corona-die-unendliche-pandemie-teil-1-das-problem-mit-den-tests/
Deine Falsch-Positiv-Rechnung muss ich leider widersprechen. Siehe dazu meinen Post zum Thema.
Inwiefern? Worauf würdest du kommen?
Ok, ich habe das gestern auf etwas müden Auge betrachtet. Du schreibst etwa 80%.
Ich komme auf:
Das würde sich ziemlich dicht mit deiner Rechnung decken.
Du hast ja die Wahrscheinlichkeit berechnet, dass jemand positives auch tatsächlich erkrankt ist. Nach dem selben Prinzip kann man auch berechnen, ob der positiv getestete nicht erkrankt. Im Bild habe ich das mit dem Satz von Bayes berechnet. Du hingegen hast es via Gegenereignis berechnet.
In unseren Wahrscheinlichkeitsraum müssen wir natürlich aufpassen, ob das überhaupt funktioniert. Dies kam mir auf den ersten Blick (müde und so^^) nicht so vor. Da unsere Ergebnisse fast identisch, habe ich aber nochmal einen 2. Blick drauf geworfen und deine Rechnung sollte funktionieren. Die Abweichung kommt sicher durchs Runden.^^
Hi @quekery,
ja cool, so herum geht es natürlich auch.
Schön, dass jemand diesen Ansatz mal gegengeprüft hat.
Noch schlimmer ist allerdings, dass dies niemand vor dir getan hat. Ich kenne übrigens NIEMANDEN der den Satz von Bayes schonmal gelernt oder selbst angewendet hat (einschließlich Naturwissenschaftler).
Ist eine schlimme Sache und zeigt wie die Bildungsmisere uns in eine tatsächliche Katastrophe katapultieren kann oder vielleicht schon hat.
Naja, mal schauen was noch so kommt.
Schönen Sonntag noch
Gruß
Chapper
Nun einen test direkt als falsch positiv zu bezeichnen nur weil bei der person keine starken Symptome aufgetreten sind finde ich etwas irreführend.
Der Virus ist ja trotzdem in der person und kann andere leute mit schwächerem Immunsystem heftiger erwischen.
Wenn du mit einem pcr test corona positiv diagnostiziert wurdest, ist ja die wahrscheinlichkeit das du das virus in dir hast und damit andere anstecken kannst sehr hoch, weshalb man in diesem fall aufjedenfall Kontakt zu anderen leuten meiden sollte (aus zivilcourage heraus).
In dem Zusammenhang auch Teil 2 lesen!
Gruß
Und das ist nur ein Problem mit den Tests. Die Tatsache, dass man das unspezifische E-Gen als Zielsequenz hat, das auch bei anderen Coronaviren "anschlägt" kommt noch dazu.
Ausserdem sind die Tests viel zu sensitiv.
Siehe dazu mein Artikel über die PCR-Tests
https://peakd.com/hive-121566/@stayoutoftherz/ueber-die-pcr-tests
Ja richtig,
Kreuzreaktionen mit anderen Coronaviren sind nicht ausgeschlossen.
Hinzukommt natürlich, dass der Nachweis eines Virus noch lange keine Krankheit anzeigt.
Bei Corona haben wir den kuriosen Fall, dass oft die Krankheit erst nachgewiesen wird, die Betroffenen aber selbst nichts merken. Das heißt die Prädiagnostik deutet oft nicht auf eine Erkrankung hin, diese wird erst durch den Test "impliziert". Das ist wie als könnte ich problemlos laufen, springen und schwimmen, nach einer Röntgenuntersuchung attestiert man mir aber ein gebrochenes Bein.
Ist die Diagnose dann relevant für mich???
Ausserdem problematisch sind die geringen Fallzahlen in der Bevölkerung. Zwar ist in Deutschland statistisch gesehen einer von 325 Bürgern infiziert, aber "nur" einer in 9000 auch daran gestorben. D.h. die Wahrscheinlichkeit an Corona zu sterben ist vergleichbar mit der Wahrscheinlichkeit eines Todes durch Blitzschlag (1:12000). Hinzukommen die Zahlen vom CDC wonach nur 6% der vermeintlichen Coronatoten in den USA auch direkt an Corona verstorben sind. Nehmen wir dies in unsere Rechnung auf habe ich eine 1:150000 Wahrscheinlichkeit direkt am Virus zu sterben. Der Tod durch Blitzschlag ist somit 12,5x höher als ein direkter Tod durch Corona.
Ich denke wir haben ein enormes Problem mit dieser "Pandemie", denn auf der einen Seite kann der Test eine hohe Fehleranfälligkeit haben. Dies ist auch klar, wenn die Häufigkeit einer Krankheit geringer ist als der Fehler der Messung.
Auf der anderen Seite ist dies aber nicht klar abschätzbar, weil viele Coronafälle symptomlos sind. Ich habe in meinem zweiten Post zum Thema gezeigt, dass es Länder mit niedrigem BMI etc. gibt wo oft nur wenige Fälle registriert wurden. Wahrscheinlich gab es da aber genauso viele Infektionen wie sonstwo, nur dass dies sich aufgrund weiterer Faktoren nicht ausprägen konnten.
Demnach gehe ich sogar davon aus, dass 1) der Test schon "richtig" ist und 2) sogar viel viel mehr Leute damit bereits infiziert sind oder infiziert waren. Die frühstückt man jetzt einfach mit ab und attestiert, wie in meinem obigen Bsp., ein "gebrochenes Bein", was aber de facto irrelevant ist.
Ich möchte keine Krankheiten relativieren oder dazu animieren leichtfertig damit umzugehen. Tatsächlich haben Menschen oder gar Bevölkerungen (wie die USA) mit einer problematischen Gesundheitssituation (z.B. in Folge von Übergewicht oder einem geringem Fitnesslevel oder eben schweren Vorerkrankungen) mitunter ein heftiges Thema mit Corona. Dies kann dann zu dramatischen Verläufen mit schweren Folgeschäden und eben auch Tod führen. Dies ist unbestritten. Für einen durchschnittlich gesunden Menschen stellt es aber, meines Erachtens nach, nur ein geringes Risiko dar.
Hoffen wir, dass irgendwann wieder sowas wie Normalität (ich meine nicht diese "Neue Normalität" von der alle sprechen) eintritt.
Besten Gruß
Chapper
Wow is a very effective probabilistic method, perhaps the problem that we currently present in the world is the effectiveness of testing to determine whether or not the virus is in our body, we know that the incubation period is approximately ten days and in that time people can present symptoms, but the genetic load of the virus is not large enough to detect it, this is where the problem comes, these people are isolated in the first instance, but what happens with the asymptomatic? How much is the number? 'Could it be included in the equation? We don't really... we don't have an exact number because those people don't have symptoms, it's impossible to determine.
Another big problem is the rapid tests, some are effective but most are not, for example in my country a person has mild symptoms and is tested and the result is negative, the doctors must tell him to go home because they do not have strong symptoms and is negative on the test, however it turns out that that person does have the virus and here is this other big problem, because that person leaves the hospital believing he has no virus and goes out to the street to spread the virus even more.
So as much as we have numbers and many statistics and probabilities, it is impossible to determine how many people we have infected worldwide. We may have a proximate but never an exact number.
The truth is I had a lot of fun reading your publication is impressive, fantastic and unique.. thank you for sharing this with the community.
Greetings!
Hey @carloserp-2000,
thank you for the comprehensive reply.
That's the root of the tragedy!
Even though the Bayes method indicates a much lower rate of infected people (in Venezuela for instance about 95% of the tests is false-positive) I assume many more people are infected. This is not covered by Bayes due to a prerequisite is that there are clear symptoms or undoubtedly sick people. For instance, if you suffer from a rare disease, let's say one person in 10000 and you show the symptoms which primarily belong to the disease then a test with high specificity and sensitivity would show the right result. Nevertheless, if you apply the test to 10000 healthy people you will receive a lot of false-positives. This is a really hard situation for physicians. Can you trust the test? Can you trust the symptoms? The improvement of the tests will change almost nothing. A better idea would be to improve pre-diagnostics. No random testing, specific testing. With this approach, you will yield more reliable results.
Stay healthy and thanks for reading (sorry I was too lazy to write it in English, maybe I will create another version in English, or maybe Spanish ;-)
Best Regards
Chapper
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Please consider using the STEMsocial app
app and including @stemsocial as a beneficiary to get a stronger support.
Thanks you!