
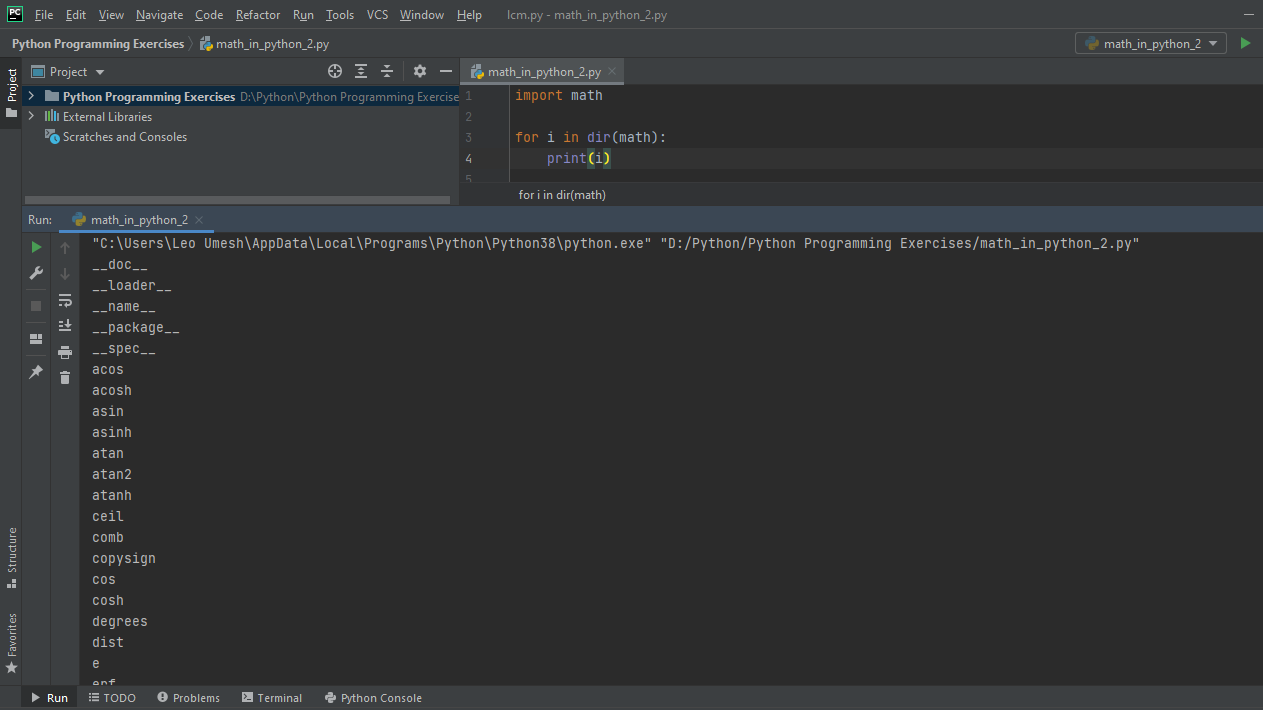
In my last post, I wrote about the basic introduction of the math module in python programming and also discuss about some basic functions to perform certain mathematics operation. In this post, we will see about the some other functions in the same module. Lets use dir() function to see the list of funtions within our math module. We will use for loop to iterate over each loop.
for i in dir(math):
print(i)
You can see the following output while executing the above code. These are the list of functions provided by the math module that you can use for performing certain operations. You can see a lot of other functions as well when you scroll down the output window.
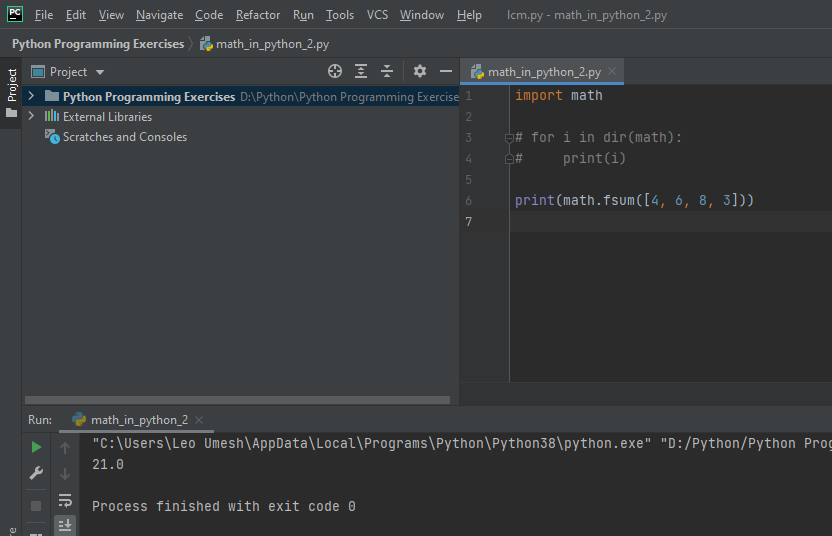
We know lists, tuples and arrays are important data structures in python. One of the function that is provided by math module is fsum() that returns the sum of all items in these iterables. For example print(math.fsum([4, 6, 8, 3])) will return output as 21 as below:
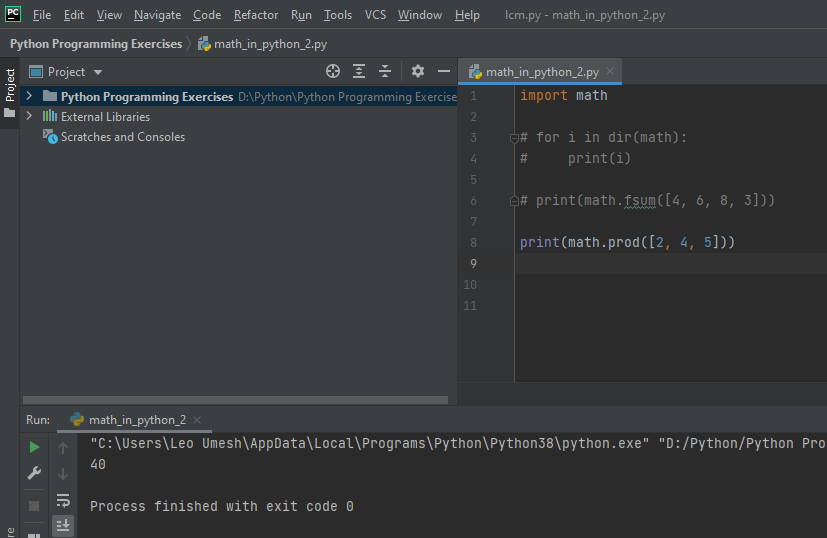
In the same way you can use prod() to find the product of items in lists, tuples or arrays. For example you can use this syntax print(math.prod([2, 4, 5])) to find the product of all numbers in a list. The outuput should be 40 in this case and same can be seen below.
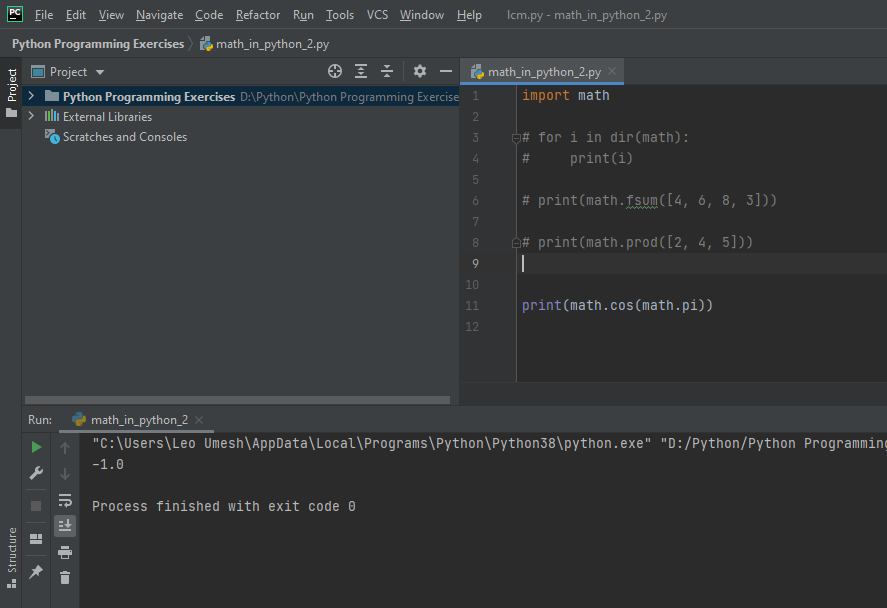
Also you can use this module for performing trigonometric operations. Lets try to find the value of cosπ which is -1. In python it can be done using the following syntax: print(math.cos(math.pi)). Following output can be seen in execution.
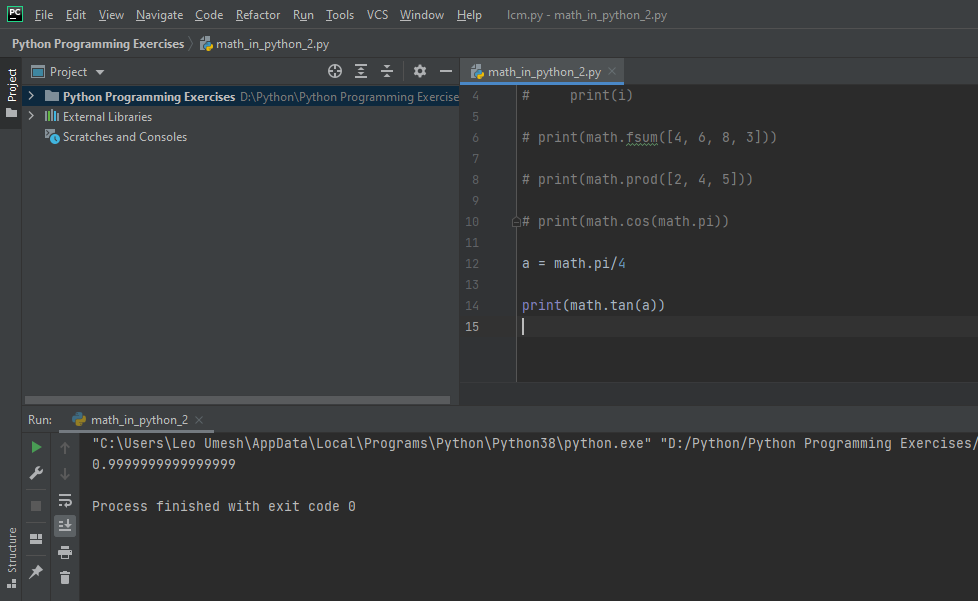
In the same way you can use tan() function to find the tangent value of any number. We know tan 45° is 1. In following code we will express 45° as (π/4) and see the same output. The code is:
a = math.pi/4
print(math.tan(a))
The output is:
Apart from these stuffs, you can use math module to perform logarithmic operations, hyperbolic functions (trigonometric functions on hyperbolas), other special operations like finding Gaussian value, Euclidean distance and so on.