I'm a strong N on Meyers Briggs. I love patterns and the nature of relationships between seemingly unrelated things. I always try to reverse engineer systems, be it behavior, business process, or how a machine works.
This book talks about symmetry in nature, and has a fascinating section on how the human as a machine processes light and information - consciousness is on delay. Below are tidbits. Author won the Nobel Prize in Physics, and writes for the layman. Pasting notes here to share. No opinions - just cool reading.
NOTES FROM A Beautiful Question by Frank Wilczek
From the regularity and order of the Solar System—with all its planets revolving around the Sun very nearly in circles, all in common plane, all in the same direction—Newton surmised, in the “General Scholium” that concludes the Principia, that the initial conditions had been mindfully arranged: This most elegant system of the sun, planets, and comets could not have arisen without the design and dominion of an intelligent and powerful
The great twentieth-century mathematician and physicist Hermann Weyl, whose books were a big part of my education, put it this way, in what I think is among the most beautiful, as well as most profound, passages in all of literature: The objective world simply is, it does not happen. Only to the gaze of my consciousness, crawling along the lifeline of my body, does a section of this world come to life as a fleeting image in space which continuously changes in time.
If Parmenides and Weyl are right, and space-time as a whole is the primary reality, then we should aspire to a fundamental description of its totality. In such a description, there would be no place left for initial conditions.
In Maxwell’s model, when magnetic vortex atoms spin, they become oblate—flattened at the poles, fattened at the equator, like Newton’s spinning Earth!—and push around the electric conducting spheres.
Maxwell’s law, as I call it, says that electric fields that change in time produce magnetic fields.
Thus an excitation in electric and magnetic fields can take on a life of its own, with the fields dancing as a pair, each inspiring the other.
Gauss’s law is, of course, very much like the electric Gauss’s law, but with the additional simplification that there can be no magnetic charge! It tells you magnetic fields have no seeds—magnetic lines of force can never end, but must either continue forever, or close on themselves.
The most dramatic prediction of Maxwell’s theory, that electric and magnetic fields could take on a life of their own and propagate in self-renewing waves, had not been verified.
The solutions of Maxwell’s equations describe much more than visible light. There are solutions where the oscillations between electric and magnetic fields take place over different distances (wavelengths). The visible spectrum corresponds to a narrow range of wavelengths within the infinite continuum of pure electromagnetic waves.
e already mentioned Hertz’s pioneering work, which gave us radio waves and blossomed into radio technology. Radio waves are “light” with much longer wavelength, and lower frequency, than visible light. In other words, in radio waves the oscillations between electric and magnetic fields take place more gradually in space, and more slowly in time
equations, and then finding (to our delight and astonishment) that the equations have a lot of symmetry, we propose equations with enormous symmetry and then check to see whether Nature uses them. It has been an amazingly successful strategy
Maxwell’s equations gave us an entirely new understanding of what light is, and predicted the existence of unsuspected forms of radiation, which are new kinds of “light.” They led directly to radio, and inspired several other major technologies. Maxwell’s equations also mark a great advance toward the answer to our Question, for they display beautiful ideas deeply embodied in the world. Their beauty derives from many sources: from the way they were discovered, from their shape, and from their power to inspire other good ideas.
Symmetry of Equations Study of Maxwell’s equations brought out an essentially new idea that had not really played a big role in science before. That is, the idea that equations, like objects, can have symmetry, and that the equations Nature likes to use in her fundamental laws have enormous amounts of symmetry. Maxwell himself was unaware of that idea. So this is most definitely an example of getting more out than was put in! What does it mean to say that equations have symmetry? While the word “symmetry” has various, often vague meanings in everyday life, in mathematics and physics “symmetry” has come to mean something quite precise. In those contexts, symmetry means Change Without Change. That definition may sound mystical, or even paradoxical, but it means something quite concrete. Let’s first consider how that strange definition of symmetry applies to objects. We say an object is symmetric if we can make transformations on it that might have changed it, but in fact do not. So, for instance, a circle is very symmetric because you can rotate a circle around its center, and though every point on it moves, overall it remains the same circle; whereas if you took[…]
One can also work in the opposite direction. We can start with symmetry, and get to objects. For example, we might ask for curves that are unchanged by rotations around some point, and then discover that circles are the unique embodiment of that symmetry. The same idea can be applied to equations. Here’s a simple equation: X=Y . . . which you can see is neatly balanced between X and Y. You’d be tempted to say it is symmetric. And indeed it is, according to the mathematical definition. For if you change X into Y and Y into X, you get a different equation, namely, Y=X This new equation differs in form, but it has exactly the same content as the old one. So we’ve got a Change Without Change: symmetry. On the other hand, when we interchange X and Y, the equation X=Y + 2 changes into Y=X + 2, which does not mean the same thing at all. So that equation is not
They are the circles defined by their own highly evolved rotations. In this way Maxwell’s equations embody a perfect correspondence: equations symmetry It is not a great stretch to see this relationship as an instance of our desired Real Ideal In modern physics we have taken this lesson to heart. We have learned to work from symmetry toward truth. Instead of using experiments to infer equations, and then finding (to our delight and astonishment) that the equations have a lot of symmetry, we propose equations with enormous symmetry and then check to see whether Nature uses them. It has been an amazingly successful strategy. This chapter’s themes of connection, symmetry, and light come together in the art of the mandala. Mandalas are symbolic representations of the Universe. They are used as tools for meditation and trance. They typically display large-scale symmetry among connected, intricate parts, and are often colorful. Plate R provides, I think, a fitting conclusion.
Maxwell’s equations changed space from a receptacle into a material medium—a sort of cosmic ocean. No longer a mere Void, space is filled with fluids that run the world
Like the impact of more conventional works of art, that impression is easier to experience than to explain. Paradoxically, there’s a word to describe beauty that can’t be described in words—“ineffable.” Having experienced the ineffable beauty of Maxwell’s equations, one would be disappointed if they were wrong. As Einstein said in a similar context, when asked whether his general theory of relativity might be proved wrong, “Then I would feel sorry for the good Lord.” Beauty and symmetry: Deeper appreciation of the Maxwell equations, acquired over several decades following their discovery, led to a complementary, more intellectually precise perspective on their beauty. They are a very symmetric system of equations, in a precise mathematical sense of that word, as we’ll discuss. The lessons drawn from the Maxwell equations—that equations can display symmetry, and that Nature loves to use such equations—
Spiders have poor vision, so they would not begin from the starting point that our visual perception suggests to us: a world of unconnected objects free to
are infinitely different. By comparing the totality of what’s out there to the information we capture, we can formulate what’s been lost quite precisely. And then we can think intelligently about how to recover some of
Plate W unpacks that description. The electric and magnetic fields at any point have both magnitude and direction, so we can draw them as colored arrows emanating from the point. Now if we did that at every point in space, we’d get quite a mess of overlapping arrows, so in the picture only the fields along one line are shown. If you imagine this whole pattern moving in the direction of the black arrow, you’ll see that at every point the electric fields (in red) change and the magnetic fields (in blue) change. As we discussed in the preceding chapter, changing electric fields produce magnetic fields, and changing magnetic fields produce electric fields. You can see how if things are just right, the moving disturbance might be self-generating—that is, that the change in the electric fields makes the magnetic fields change in such a way as to make the electric fields that made the magnetic fields, and the whole process takes on a life of its own. It’s a feat worthy of Baron von Münchausen, who—according to Baron von Münchausen—can pull himself up by his own bootstraps. But for electromagnetism it’s not a tall tale[…]
any direction. Pure electromagnetic waves with wavelengths in a specific, narrow range—from about 370 to 740 nanometers, quantitatively—are the raw material for human vision
Color, as we sense it, is a way of preserving some very useful information about the temporal microstructure of the signal that survives the averaging process. Colors give us information about the variation of electromagnetic fields over much smaller time intervals, in the range 10−14−10−15—a few millionths of a billionth—of a second! Because no everyday objects can move very far, or do anything noteworthy, during such tiny intervals of time, the two kinds of time information, the kind encoded in the changes from one snapshot to another, and the kind encoded in colors, are quite independent. For instance, when we perceive pure spectral yellow, our eyes are telling us that the incoming electromagnetic waves are pure waves that repeat themselves about 520,000,000,000,000 times per second. When we perceive spectral red, the message is that repeats occur about 450,000,000,000,000 times per second
Having examined the “what” and “how” of color vision, we’re ready to address the question “Why?” Two “why” questions naturally arise: Why do humans, and many other creatures, care so much about ultrarapid oscillations in electromagnetic fields? Now if I’d posed that question in the form “Why do humans, and many other creatures, care about color?” so many answers would spring to mind that the question would seem ridiculous. But if we ask it in the first form, which sho
n elegant way to do that is to manipulate the signal in time. For example, we can encode Green as added shimmering, pulsation, or generally temporal modulation—time-varying textures—in the perceptible colors, whose local intensity is proportional to Green in the original image. Let’s reflect on what we’re doing here
As we’ve seen, there’s a double infinite of colors out there, awaiting our cleansed perception. The reasons technology has mainly settled on three are: 1. Three basic colors enable us, as Maxwell taught us, to synthesize any perceptual color. 2. Two basic colors won’t do that job. 3. It’s simplest and cheapest to use the smallest number that’s sufficient.
Are there Infinities to which we’re shuttered? Yes. The world of physical colors is a space of doubly infinite dimension, of which we perceive only a three-dimensional projection. Can we unveil them? Yes. The question is not whether that is possible, for it certainly is, but how to do it, in a practical way.
Although we have the impression that our vision reveals the instantaneous state of the world, giving us a continuous, seamless reflection of events as they happen in time, the reality is different. Our
vision is more nearly a series of snapshots, each with an exposure time of about one twenty-fifth of a second. Our brain fills in between those snapshots, to give the illusion of continuity. Movies and television exploit this fact: If the images they present are updated fast enough, we don’t sense that they are a sequence of stills, or a rapid series of pixel updates.
What we can say for sure is that my mapping, or projection, of physical light into perceived colors matches yours, very nearly
In musical terms, the human visual range spans one octave (one doubling of wavelength). Each spectral color corresponds to a definite wavelength,
The vast bulk of the electromagnetic spectrum evades our vision altogether. We do not, for example, see radio waves, and without radio receivers we’re left unaware of their existence.
Roughly speaking, our eyes give us snapshots twenty-five times a second, and our brains create the illusion of a nonstop movie from those snapshots. That construction underlies our everyday sense of the flow of time. In the process of gathering light for those snapshots—as photographers say, during the exposure time—the light is simply added up, or integrated. Because the light arriving at different times within each time frame is lumped together, information about arrival time, within each frame, is lost.
In short: The space of color information is infinite-dimensional, but we perceive, as color, only a three-dimensional surface, onto which those infinite dimensions project.
to the same thing, it raises a profound point. Information about rapid oscillations in electromagnetic fields is important to us, as biological creatures
In plain English: The colors of objects encode what they are made of. You knew that, of course, from experience. But now you also know, in terms of fundamentals, just what it is you’ve experienced!
Each pixel in our visual field potentially supplies a doubly infinite chord, but we see only color, a three-dimensional projectio
reen, was telling something about the structure of light, as an electromagnetic signal, in time. We’re putting it back as Green, again a time signal, but slowed down, to match the pace of human information processing. We’re using time and brain to open the doors of perception.
or example, there are materials called electrochromics whose tendency to absorb light within particular spectral regions can be modulated by applying a voltage. If we fit ordinary glasses with electrochromic layers, and apply a time-varying voltage, we will be opening up new color channels
The same general ideas will allow us to open up essentially new dimensions of color vision, as seen in plate AA. Of course, before making this new information accessible, we must first collect it. The fact that digital photography and computer graphics are based on three basic colors, as opposed to more, is not
We will compare the full reality of vision’s subject matter—light—with the projection of reality that human vision captures. This was a subject that Maxwell loved, and greatly clarified. In that context, we will substantiate Blake’s visionary intuition by answering the two questions it raises: Are there Infinities to which we’re shuttered? Yes. The world of physical colors is a space of doubly infinite dimension, of which we perceive only a three-dimensional projection. Can we unveil them? Yes. The question is not whether that is possible, for it certainly is, but how
Maxwell gave us new conceptions of what light is, and of what our perception of light is. And they are very different things! As Blake anticipated, they are infinitely different. By comparing the totality of what’s out there to the information we capture, we can formulate what’s been lost quite precisely. And then we can think intelligently about how to recover some of it.
Plate W unpacks that description. The electric and magnetic fields at any point have both magnitude and direction, so we can draw them as colored arrows emanating from the point. Now if we did that at every point in space, we’d get quite a mess of overlapping arrows, so in the picture only the fields along one line are shown. If you imagine this whole pattern moving in the direction of the black arrow, you’ll see that at every point the electric fields (in red) change and the magnetic fields (in blue) change. As we discussed in the preceding chapter, changing electric fields produce magnetic fields, and changing magnetic fields produce electric fields. You can see how if things are just right, the moving disturbance might be self-generating—that is, that the change in the electric fields makes the magnetic fields change in such a way as to make the electric fields that made the magnetic fields, and the whole process takes
At any one point, as time progresses, the electric field arrow goes up and down, like the surface of water in a wave. In general, we call moving, self-generating electromagnetic disturbances electromagnetic waves. Our picture shows a particularly simple electromagnetic wave, where the pattern of electric and magnetic disturbances repeats after a certain distance (and, technically, follows a sine function). I’ll call this a pure wave, for reasons that will become clear momentarily. In that case we call the spacing between the repeats the wavelength of the wave. The pattern will also repeat in time, at a rate we call the frequency of the wave
of disturbance that’s still a solution. That amounts to adding your original solution to itself. You can also add one solution to another, and the result is a solution. These mathematical possibilities correspond to the physical possibilities of turning the brightness of a light beam up or down (multiplication) or combining one beam with another (addition). We know, from experience, that turning up the brightness and adding are things you can do with light beams. So we’d be in trouble, trying to identify light as a form of electromagnetic waves, if we couldn’t do them with electromagnetic waves. Fortunately, we can. Finally, let’s match up the details of Maxwell’s verbal description, quoted above, with our pictorial version. You see, in the picture, that the electric and magnetic fields are perpendicular (or, in other words, at right angles) to each other, and that the direction of motion is perpendicular to both. That’s exactly the geometry Maxwell describes in words. And the rapid, alternate (i.e., up-and-down) oscillations he mentions are just what you will observe, at any fixed point, as the wave progresses.
We have pure electromagnetic wave solutions of the Maxwell equations for any wavelength, traveling in any direction. Pure electromagnetic waves with wavelengths in a specific, narrow range—from about 370 to 740 nanometers, quantitatively—are the raw material for human vision. They correspond to the pure light revealed in Newton’s prismatic spectrum. In musical terms, the human visual range spans one octave (one doubling of wavelength). Each spectral color corresponds to a definite wavelength, as shown in plate P.
On the other hand, almost all of the Sun’s electromagnetic radiation that penetrates Earth’s atmosphere is concentrated near the visible part of the spectrum, so that’s the most useful part for earthbound creatures to be attuned to. It’s where the signal is turned on, so to speak. For the moment, let’s concentrate on the resource that our Sun’s illumination gives us in abundance, and
consider just the visible part of the spectrum. Does our perception take full advantage of that resource? No. Not by a long shot.
giving us information about rapid variations in the electromagnetic fields that enter our eyes. To avoid a possible confusion, let me emphasize that the time information carried by color is very different from, and complementary to, the time information we use in our everyday reconstruction of the order of events in time. Roughly speaking, our eyes give us snapshots twenty-five times a second, and our brains create the illusion of a nonstop movie from those snapshots. That construction underlies our everyday sense of the flow of time. In the process of gathering light for those snapshots—as photographers say, during the exposure time—the light is simply added up, or integrated. Because the light arriving at different times within each time frame is lumped together, information about arrival time, within each frame, is lost. Color, as we sense it, is a way of preserving some very useful information about the temporal microstructure of the signal that survives the averaging process. Colors give us information about the variation of electromagnetic fields over much smaller time intervals, in the range 10−14−10−15—a few millionths of a billionth—of a second! Because no everyday objects can move very[…]
of time, the two kinds of time information, the kind encoded in the changes from one snapshot to another, and the kind encoded in colors, are quite independent. For instance, when we perceive pure spectral yellow, our eyes are telling us that the incoming electromagnetic waves are pure waves that repeat themselves about 520,000,000,000,000 times per second. When we perceive spectral red, the message is that repeats occur about 450,000,000,000,000 times per second. Or rather, our eyes would be telling us those things if they didn’t conflate the possible message “spectral yellow” with a manifold of other possible mixtures of colors that likewise look yellow, and the possible message “spectral red” with a (different) manifold of mixtures that look red. The actual message they convey is ambiguous because many possible inputs give the same output! A true analysis of the incoming signal as to color must reveal the same information as Newton’s prismatic analysis. A true analysis, that is to say, would resolve the incoming signal into its pure spectral components, each having its own independent strength. To report the result of such an analysis, we would need to specify a continuous infinity of numbers, one for the strength of
each pure spectral component. Thus space of potential color information is not merely infinite, but infinite-dimensional. Instead, our eyes’ projection of this information captures, as Maxwell discovered, just three numbers. In short: The space of color information is infinite-dimensional, but we perceive, as color, only a three-dimensional surface, onto which those infinite dimensions project.
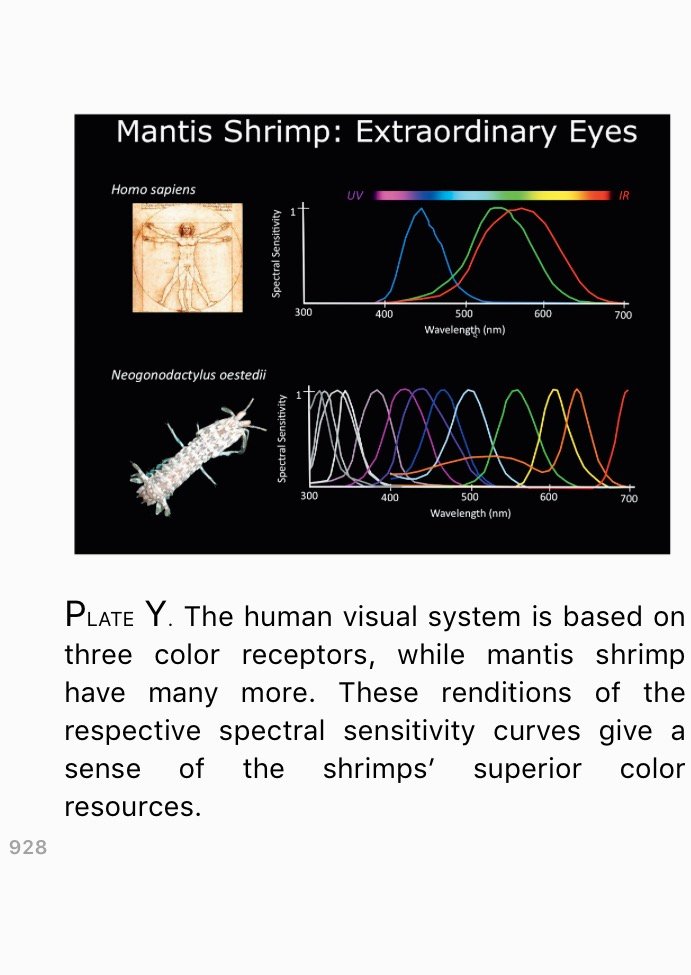
unleash little pulses of electricity, which are the data our brains use to construct our sense of vision. Now, the probability that a given unit of light will be absorbed depends both on its spectral color and on the properties of the receptor molecule. One kind of receptor is most likely to absorb light in the red part of the spectrum, another peaks in green, and the third in blue, though their tuning isn’t sharp (see plate Y). At common levels of illumination there are lots of photons, so there are many absorption events, and these probabilities get translated into three accurate measures of the amount of power the incoming light contains, averaged over three different spectral ranges.
In this way, we become sensitive not only to the overall amount of light arriving, but also to its composition. If it is spectral red light, it will stimulate firing from the red-peaked receptors more than the others, and result in a completely different signal than spectral blue light (which, of course, stimulates the blue-peaked receptors most). On the other hand, any sort of incoming light that has the same ability to stimulate each of the three kinds of receptors—in other words, that gives the same three weighted averages—will be “seen” as the same by each
Why do humans, and many other creatures, care so much about ultrarapid oscillations in electromagnetic fields? Now if I’d posed that question in the form “Why do humans, and many other creatures, care about color?” so many answers would spring to mind that the question would seem ridiculous.
y is vision so different from hearing? After all, both senses are concerned with the information carried to us in vibrations, arriving as waves. Vision is concerned with vibrations of electromagnetic fields, hearing with vibrations of air. But the ways we perceive chords of light and chords of sound are profoundly, qualitatively different. Let me be precise about that. When we receive several pure sound tones sounding together, we hear chords in which the tones retain their individual identity. Within a C major chord, you can hear the C, the E, and the G separately, and you’ll certainly notice a qualitative difference if any one of them is absent, or if it is notably louder than the others.
What we can say for sure is that my mapping, or projection, of physical light into perceived colors matches yours, very nearly. We both see many mixtures of spectral colors as yellow, and many others as magenta. Most
The central result to emerge from these studies is that by using just three colors in the inner strip, we can match any color in the outer one. Thus, for example, we can use spectral red, green, and blue, in appropriate proportions, to get orange, mauve, chartreuse, puce, azure, burnt peony, or any other color you care to name.
The three base colors need not be red, green, and blue (RGB)—almost any three will do, including mixtures, as long as they are independent. (If one of your base colors can be obtained as a mixture of the other two, it doesn’t enable new possibilities.) On the other hand, we do need three base colors. If you restrict yourself to two base colors—no matter what they are—then most colors can’t be matched by mixing them.
Power of three as a systemcolors” given as an option, it refers to millions of different ways of adjusting the relative intensity of those sources. In other words, one samples millions of different points, but all within a three-dimensional space.
The fact that one can synthesize all perceived colors by mixing three is widely exploited in modern color photography, television, and computer graphics. For example, in color photography three kinds of color-sensitive dyes are used. In computer displays, there are three kinds of color light sources. When you see “millions of
For artists, the possibility to obtain the same perceptual color in many different ways opens up creative possibilities.
on a life of its own. It’s a feat worthy of Baron von Münchausen, who—according to Baron von Münchausen—can pull himself up by his own bootstraps. But for electromagnetism it’s not a tall tale, nor magic realism, but realistic magic.
A very important property of electromagnetic waves is that you can multiply and add them. That is, if you have an electromagnetic wave solution of Maxwell’s equations, and multiply the electric and magnetic fields in it by a common factor, the result will still be a solution of Maxwell’s equations. So if you make all the fields in a solution twice as big, for example, you get another kind
The vast bulk of the electromagnetic spectrum evades our vision altogether. We do not, for example, see radio waves, and without radio receivers we’re left unaware of their existence.
What would a full analysis of the signal entering our eyes consist of? The answer to that question has two aspects, which are quite distinct. One is the spatial aspect. The signal contains information about the directions of light rays as they arrive from different objects. We use that information to form images. The other is the color aspect. It captures a different sort of information. We can have images in black and white, and we can have color patterns—in the extreme case, simply eye-filling, uniform colors—that don’t make images.
While imagery reveals information about what’s happening in space, color is telling us about what’s happening in time. Specifically, color is
complete the story, I should also mention another kind of electromagnetic information that’s on offer, but also disregarded, within the signal entering our eyes. Referring back to plate W, you will notice that the electric fields (red) are oscillating in a vertical direction, while the magnetic fields (blue) are oscillating in a horizontal direction. There is also another solution, where you rotate the whole pattern by 90 degrees, so the electric fields are horizontal and the magnetic fields vertical. This rotated solution oscillates at the same rate as the original solution, so it represents the same spectral color. But it is physically distinct. The new property that corresponds to this distinction is called the polarization of the wave. Thus the electromagnetic information entering our eyes at each image point is infinite-dimensional twice over, because for each spectral color there are two possible polarizations, each of which can occur with an independent strength. Human vision overlooks that doubling because human eyes cannot distinguish between different polarizations of light.
Octaves?The central result of Maxwell’s color matching experiments, that mixing three basic colors can generate any perceptual color, reveals a deep fact about the “what” of human perception, but it also raises the question “How?” A beautiful and instructive answer to the “how” question emerged in the mid-twentieth century, as biologists explored the molecular basis of color vision. (It’s fun to notice that physicists figured out the biology, and then biologists figured out the physics.)
The central result in the molecular story of vision is that three different kinds of protein molecules (rhodopsins) extract our information about color. When light impinges on one of these molecules, there is a certain probability that the molecule will absorb a unit of light—a photon—and change shape. The shape changes
of our color receptors, and will therefore result in the same visual perception. It takes three numbers to get a match: on that, the molecules agree with the color tops!
There are also women who see a four-dimensional space of colors: tetrachromats. They have an extra receptor protein, which is a mutation of the usual ones. They can discriminate among mixtures of spectral colors that most people perceive as indistinguishable. This ability seems to be rare, and has not been much studied.
On the other hand, many types of insects and birds have four or even five color receptors, including sensitivity to ultraviolet, and also sensitivity to polarization. Many flowers are patterned and colored vividly in the ultraviolet, to seduce their pollinators. Within the sensory universe of color, they explore dimensions that evade our awareness.
Depending on the species, they can see between twelve and sixteen color dimensions. Their range of sensitivity extends into the infrared and the ultraviolet (see plate Y), and also encodes some information about polarization.
the species with the most advanced color vision are generally the most colorful.
How do such small crustacean brains cope with such a gush of sensory input? That question is a subject of current research. It seems probable to me that they use the technique known to information engineers as “vector quantization”—a piece of jargon that I’ll now unpack. Humans fill in their three-dimensional color space very finely. We are able to distinguish nearby points in that space, and thus to experience millions of distinct color perceptions. Mantis shrimp probably use a much coarser representation, with input from large regions of their sixteen-dimension space all giving the same output. Where we can resolve points within a relatively small space, they locate blobs dividing up a much bigger space. We make a very crude (three-dimensional) projection of the infinite-dimensional electromagnetic input, but survey that projection accurately, while the mantis shrimp makes a more sophisticated projection, but surveys it crudely
In plain English: The colors of objects encode what they are made of.
The physics of hearing is the physics of sympathetic vibration, as we discussed earlier. There’s a good physical reason why light must be treated differently. The oscillations of electromagnetic fields in visible light are far too rapid for any practical mechanical system to follow. So the strategy we use in hearing, where vibrations of air get channeled to set up sympathetic vibrations in our heads, won’t work. To get in tune with the vibrations of light, we need to use much smaller, nimbler responders.
For light, the useful receptors are individual electrons. But in the subatomic world of electrons, quantum mechanics comes in, and the rules of the game change. The transfer of information from light to electrons can come about only through the transfer of some of the light’s energy. According to the quantum rules, however, such energy transfers occur in discrete “all or none” events—absorption of photons—that occur at unpredictable times. These effects make the information transfer a less faithful transcription, and one that is harder to control.
And that—when it is spelled out more rigorously—explains why our perception of light’s time-structure, as encoded in color, is cruder than our perception of sound’s time-structure, as encoded in musical harmony. Quantum mechanics is to blame. By having several different kinds of receptors, attuned to different features, we rescue some of light’s time information. But there is no visual analogue to the vibrating membranes of the inner ear where, for sound, it is all laid out bare, as on the keys of a player piano.
Vision is primarily a space sense, while hearing is primarily a time sense, for good physical reasons.
And now let’s make a leap of imagination, ascending from the solid ground of “what,” “how,” and “why,” into the dreamscape of “what if,” “how to,” and “why not.”
The human mind is our ultimate sense organ. Mind has discovered that there are invisible infinities hidden in light. Our perception of color projects the doubly infinite-dimensional space of physical color onto the three-dimensional wall of our inner Cave. Can we escape that Cave to sample the additional dimensions?
It’s easy to express Galileo’s observation as a symmetry. We change the world—or a big part of it, like the interior of a large ship—by moving everything at a common velocity, without change to the way things behave. We call that kind of transformation, in Galileo’s honor, a Galilean transformation. Correspondingly, we call his postulate of symmetry Galilean symmetry, or Galilean invariance. According to Galilean symmetry, we can change
Arthur C. Clarke’s third law of prediction reads: Any sufficiently advanced technology is indistinguishable from magic.
We can also roughly “predict” the size and shape of Earth’s orbit around the Sun, from quite a different kind of consideration. That is: if the size and shape of that orbit were very different, intelligent life would not be around to observe it! For under those circumstances, life in anything close to the form we know it would be impossible (or at least very difficult). Among other problems: if the orbit is much smaller, surface water boils away; if the orbit is much bigger, surface water freezes; if the orbit is not nearly circular, one has wrenching changes in temperature. Arguments like that, which promote the conditions for our existence into principles, are called anthropic arguments. Taken in their most general form, anthropic arguments beg many questions. First of all, who is the “our” in “our existence”? If we require everything that is necessary for the existence of, say, Frank Wilczek—or alternatively, you, the reader—we will be making principles out of many special circumstances that we really don’t want to regard as fundamental features of the Universe, the Solar System, or even Earth. A more reasonable approach, possibly, is to base anthropic “predictions” on the looser[…]
s Maxwell recognized, if atoms and molecules operated on the same principles as the Solar System, the world would be very different. Every atom would be different from every other, and every atom would change over time. Such a world wouldn’t have chemistry as we know it, with definite substances and fixed rules. It is not immediately obvious what makes atomic systems behave so differently. In both cases we have a massive central body attracting several smaller ones. The forces in play, gravitational or electrical, are broadly similar—both decrease as the square of the distance. But there are three factors which make the physical outcome very different, giving us stereotyped atoms but individualized solar systems
in the quantum world of atoms, a strange world that also happens to be our own, a miracle occurs. Old ideas come back to life, wearing splendid new forms. In their resurrected forms those ideas attain new levels of precision, truth, and, surprisingly, musicality.
From the heart of matter, music: There is no logical reason to expect that the mathematics developed to understand music should have anything to do with atomic physics. Yet the same concepts and equations turn out to govern both domains. Atoms are musical instruments, and the light they emit makes their tones visible. From beautiful laws, beautiful objects: The basic laws do not postulate the existence of atoms. Atoms emerge from the laws, and they emerge as beautiful objects (see plate CC). Physical atoms, mathematically described, are three-dimensional objects that will, to the animating spirit of an artist, yield images of exceptional beauty. From dynamics, permanence: The basic laws are equations that describe how things change in time. But those equations have some important solutions which do not change in time. Those solutions, and those alone, describe the atoms which build up our everyday world, and ourselves. From continuity, discreteness: The wave functions that describe electrons in atoms are fields of probability (probability distributions) that fill space. They are continuous, and cloud-like. But the stable cloud patterns are discretely different, and bear the stamp of Number
The natural frequency is also called a resonant frequency, for the following reason. If the frequency of your driving force is close to the natural frequency of some pattern, that pattern will leap out in powerful response. For then, and only then, does the external driving force match up with the internal forces, cycle after cycle, to build up the strength of the motion. Anyone who’s pumped their legs and straightened their body to build up the motion of a swing, or pushed a child on one, knows how important that is.
Gongs produce an evolving chord, gradually shedding complexity until it becomes a single tone, because there are several long-lived patterns that decay at different rates.
comes in units, photons, that cannot be broken down further. The amount of energy in a minimal unit, or quantum, of light is proportional to the frequency of the
An important part of good scientific strategy is to distinguish between problem areas that might be ripe for a grand synthesis, and problem areas where a more opportunistic approach will be more fruitful. A successful theory of something can be more valuable than an attempted Theory of Everything.
is impossible, according to quantum theory, to answer both questions at the same time
You get probabilities, not definite answers. You don’t get access to the wave function itself, but only a peek at processed versions of it.
mutually incompatible. Thus no one approach, however clever, can provide answers to all possible questions. To do full justice to reality, we must engage it from different perspectives. That is the philosophical principle of complementarity.
The equation that describes how the wave function of an electron evolves in time is called the Schrödinger equation. The Schrödinger equation, regarded as a piece of mathematics, is closely related to the equations we use to describe musical instruments.
In that spirit, because the Schrödinger equation for an electron in an atom looks very much like the equation for vibrations of a musical instrument, we should consider the solutions that look like natural vibrations. A natural vibration of the wave function turns out to mean something extremely simple and appealing for its probability cloud—namely, that it doesn’t change at all!
In human manufacturing, use of interchangeable parts was a revolutionary innovation, and hard work to achieve. How did Nature achieve it? How could uniformity, if achieved by careful adjustment, stand up to the ravages of time? And if the building blocks are supremely stable, and resistant to change, how did they arise in the first place?
We’ve seen how quantum mechanics brings discreteness, and fixed patterns, into the description of continuous objects that obey dynamical equations
To close the loop, we need to understand why the electrons in atoms are usually found in just one among their infinite variety of patterns. That’s where our third item comes in. The pattern with lowest energy—the so-called ground state—is the one we generally find, because atoms are starved for energy.
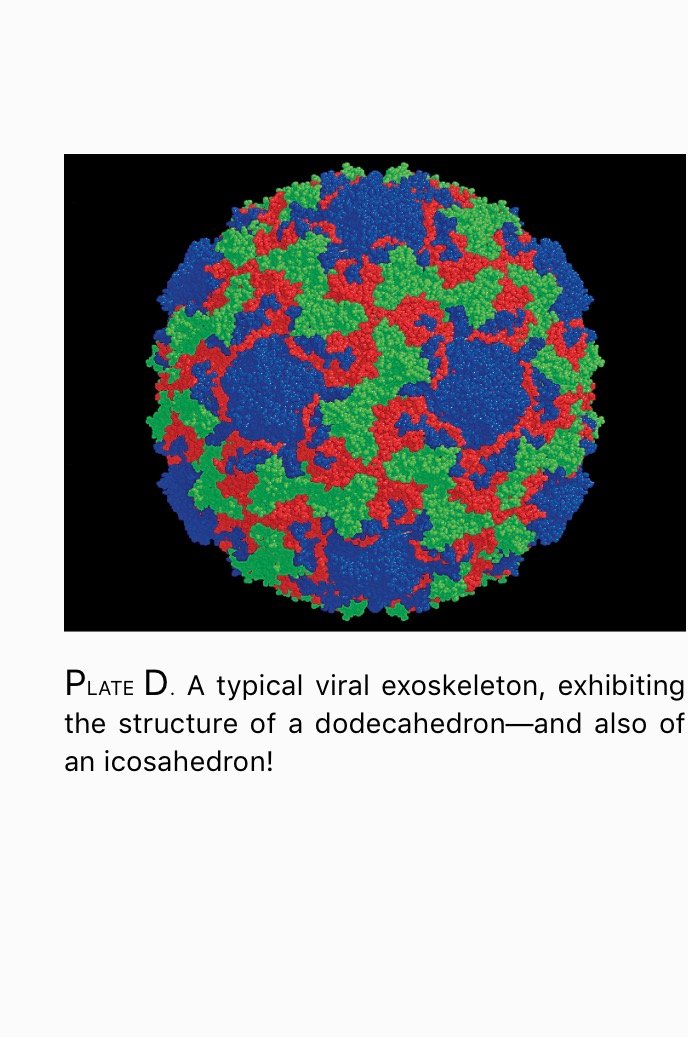
Worthy images of atoms will share, in their mixture of regularity and variation, the qualities of mandalas. They will offer, too, an awe-inspiring perspective on the assertion at the heart of mystical spirituality: That Art Thou. Because, you know, it is
Let us consider how a pure beam of light, with a definite spectral color, changes if we view it from a platform moving at constant velocity; in other words, if we make a Galilean transformation. Naturally, we still see a light beam. And that beam still progresses through space at the previous rate: The speed of light is invariant. If we began with a pure beam, with a definite spectral color, it will still appear to us as a pure beam, with a definite spectral color. But . . . It’s a different color! If we move in the same direction as the beam (thus, running away from its source), or if its source is receding from us, its color shifts toward the red end of the spectrum (or, if it started red, it will shift into the infrared). If we move in the opposite sense, the color shifts toward the blue end of the spectrum (or into the ultraviolet). The faster we move, the more pronounced the effect. The former effect is commonly encountered in cosmology because distant galaxies are moving away from us—or, as we say, the Universe is expanding. In that context, it is known as the redshift[…]
The physical essence of color, like the physical essence of tone, is a signal that varies in time. The time variation of light is too fast for our substance to follow. Its frequency is too high. And so, to make the best of a difficult situation, our sensory system processes the information and encodes a small part of it in perceived color. That code, by the end of the day, bears little trace of its origin! When we perceive a color, we see a symbol of change, not anything that changes.
We’ve been using artistic perspective as our prototype of symmetry. You can view the same scene from different places, thereby getting different perspectives. The images the scene projects can and will differ in many ways, but they all convey the same scene. Change in perspective, without change in scene, is a shining example of symmetry. In a like manner, we can view the world from a different “perspective” by giving it a constant velocity or, what amounts to the same thing, viewing it from a moving platform. When we do that, many things will come to look different, but—according to special relativity—the same laws of physics will hold good. In that sense, it will still be (a picture of) the same world. Now let us consider m
We could, more “physically,” consider viewing
All colors are one thing, seen in different states of motion. That is science’s brilliantly poetic answer to Keats’s complaint that science “unweaves a rainbow.”
If we didn’t understand the effect of the water, we’d be tempted to think that the images must convey different scenes. But if we know about water, and allow for its effect, we can count many more possible images as valid representations of our scene. We might distribute the water in different ways, for example, to mimic the effect of a fun-house mirror. We could even put our water in motion so that the images might also change with time. In short: by imagining a space-filling fluid, and allowing for its possible effects, we are able to consider a wide variety of transformed images as representations of the same scene, viewed through different states of the fluid
For our present purpose, which is appreciating how the exuberant, spontaneous creativity of electrons arises from simple rules, Pauli’s original formulation is all we need. Rule number three, in the crude form we’ll use it, is this: No more than two electrons can be in the same stationary state. (Why no more than two? That seems odd! It is a consequence of the electron’s intrinsic spin. Two electrons can both be in the stationary state, only if they are spinning in opposite directions. A more satisfying formulation of Pauli’s principle says that no more than one electron can be in the same stationary state, but includes spin as part of the description of the state.)
Anamorphic art warps the spatial structure of images. It is an excellent representation of the sorts of space-time transformations that general relativity accommodates as symmetries. The sorts of transformations that the other forces accommodate would be best represented by an art form that is less cultivated, if it exists at all. Anamorphic art leaves the color structure of its images unchanged. In anachromic art, on the contrary, we modulate the color structure of images, while leaving their spatial structure unchanged.
Color and geometry, symmetry, anachromy, and anamorphy, as ends in themselves, are only one branch of artistic beauty
Let me explain that audacious, yet manifestly valid, claim. To be concrete, let’s consider the example of a computer screen. How can we represent the information it presents? Or, in practical terms: If we’re programming a computer, how do we tell the computer what it must do to bring our viewing screen to life?
Matter tells space-time how to curve. Space-time tells matter how to move
um. So we should say instead: Energy-momentum tells space-time how to curve.
Space-time tells energy-momentum what straight is (in space-time). And so, putting it all together: Energy-momentum tells space-time how to curve. Space-time tells energy-momentum what straight is (in space-time).
Energy-momentum tells the metric fluid how to flow. The metric fluid tells energy-momentum how to flow. Electric charge tells the electromagnetic fluid how to flow. The electromagnetic fluid tells electric charge how to flow. Weak charge tells the weak fluid how to flow. The weak fluid tells weak charge how to flow. Strong charge tells the strong fluid how to flow. The strong fluid tells strong charge how to flow.
you have been perceiving extra dimensions, fields, and property spaces* every day, for years, very likely without knowing it. Any time you look at a color photograph, your brain is digesting a three-dimensional (color) property space atop ordinary space. When you watch a color movie or a television program, or interact with a computer screen, you are processing a three-dimensional property space defined over space-time
We can represent the different picture elements, or pixels, by their horizontal and vertical positions. This requires two numbers x, y. For each pixel, to support a general color perception, we must specify—as Maxwell taught us!—the intensities of three color sources. These sources are usually chosen to be forms of red, green, and
ow does space-time instruct matter to move, exactly? Its instruction, according to general relativity, is very simple: Keep going as straight as you can
According to the quark model, baryons are bound states of three more fundamental entities:
we find that many different particles reflect the same underlying material structure, captured in different states of internal motion
t a high-energy electron-positron collider, collisions of two very light particles (an electron and a positron) routinely output dozens of particles whose total mass adds up to many thousands of times the total input mass


Congratulations @alexanderchopan! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honnor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOPIf you want to support the SteemitBoard project, your upvote for this notification is welcome!