Arithmetic
We can apply recursion theorem, from the previous section, to define addition and multiplication on  .
.
Suppose we want a function 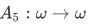 such that
such that 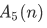 is the result of adding 5 to n. Then
is the result of adding 5 to n. Then 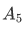 must satisfy the conditions
must satisfy the conditions
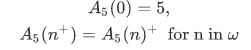
The recursion theorem assures us that a unique such function exists.
Definition A binary operation on a set A is a function from 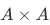 into A.
into A.
Definition Addition (+) is the binary operation on  such that for any m and n in
such that for any m and n in  .
.
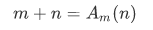
Thus when written as a relation
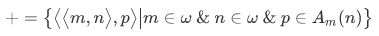
In conformity to everyday notation, we write m+n instead of
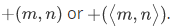 .
.
Theorem 4I For natural numbers m and n,
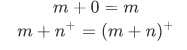
This theorem is an immediate consequence of the construction of
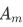 . The Theorem 4I serve to characterize the binary operation + in a recursive fashion.
. The Theorem 4I serve to characterize the binary operation + in a recursive fashion.
We now proceed to construct the multiplication operation in much the same way.
Definition Multiplication 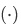 is the binary operation on
is the binary operation on 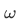 such that for any m and n in
such that for any m and n in 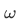 ,
,
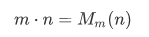
This is just an extension of Theorem 4I.
Theorem 4J For natural numbers m and n,
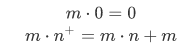
For convenience, we can now discard the
 functions, and use
functions, and use  and use Theorem 4J instead.
and use Theorem 4J instead.
We could, in the same manner, define the exponentiation operation on 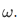 The equations that characterize exponentiation are,
The equations that characterize exponentiation are,
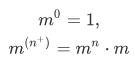
Example Show 2 + 2 = 4
We can show the addition as follow:
We have given some set-theoretic definitions of the operations of arithmetic, the next step is to verify that some of the common laws of arithmetic are provable within set theory.
Theorem 4K The following identities hold for all natural numbers.
(1) Associative law for addition
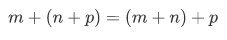
(2) Commutative law for addition
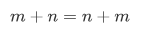
(3) Distributive law
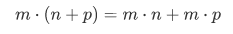
(4) Associative law for multiplication
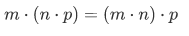
(5) Commutative law for multiplication
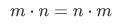
Disclaimer: this is a summary of section 4.4 from the book "Elements of Set Theory" by Herbert B. Enderton, the content apart from rephrasing is identical, most of the equations are from the book and the same examples are treated. All of the equation images were screenshots from generated latex form using typora
Thank you for reading ...


You got a 25.00% upvote from @nado.bot courtesy of @sinbad989!
Send at least 0.1 SBD to participate in bid and get upvote of 0%-100% with full voting power.