Área y perímetro. Unidades de área y el cuadrado
1. Introducción
Hace algunos días le explicaba a una estudiante de bachillerato el cálculo de áreas y perímetros de algunas figuras planas como el rectángulo, el paralelogramo, el trapecio, el triángulo y el círculo.
Toda mi explicación iba muy bien hasta que la chica me preguntó—:
Si el cuadrado es una figura geométrica de lados iguales, ¿Por qué las áreas vienen dadas en unidades al cuadrado?
Yo sonreí con sarcasmo y le dije—:
Simplemente todas las unidades que están elevadas a la potencia dos se les dice al cuadrado. Si por ejemplo tú tienes kilogramos multiplicado por kilogramos te dará kilogramos al cuadrado (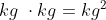
), y eso no tiene nada que ver con la figura geométrica del cuadrado.
La chica simplemente asentó moviendo la cabeza y mordiéndose mitad del labio como pensando que estaba haciendo preguntas estúpidas. Pero luego me detuve; me di cuenta que lo que yo decía no era del todo cierto, al menos en el caso de las áreas, entonces me propuse a explicarle lo mejor que podía lo que era el área de una figura geométrica, esa explicación debía ser sencilla, práctica y divertida. Después de explicarle y de hacer algunos experimentos didácticos la estudiante quedó muy satisfecha, sorprendida y contenta, y yo también.
Es precisamente ese tipo de explicación vivencial, lo que trataré de exponer en este artículo, la idea principal es que el estudiante aprenda haciendo y construyendo lo que necesita comprender, sin importar lo complicado que parezca. Espero que este trabajo, al igual que a mi alumna, sirva a mis lectores de HIVE para entender mejor el concepto de área y perímetro a nivel de bachillerato.
2. ¿Qué es un área?
Antes de responder a esta pregunta debemos saber que estrictamente hablando el área es un concepto abstracto, y su estudio profundo se encuentra en el campo de las matemáticas puras, pero en este artículo no hondaremos en tales abstracciones. Daremos una explicación sobre la base de conceptos y definiciones que se dan a nivel del bachillerato, pero que incluso es aplicable a estudios universitarios de carreras técnicas.
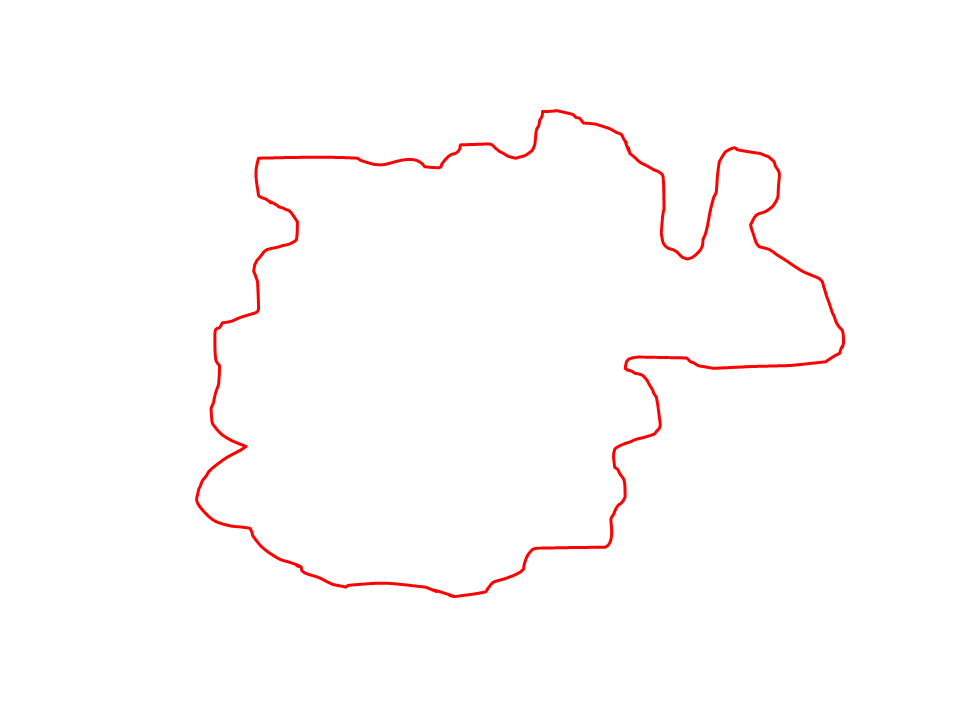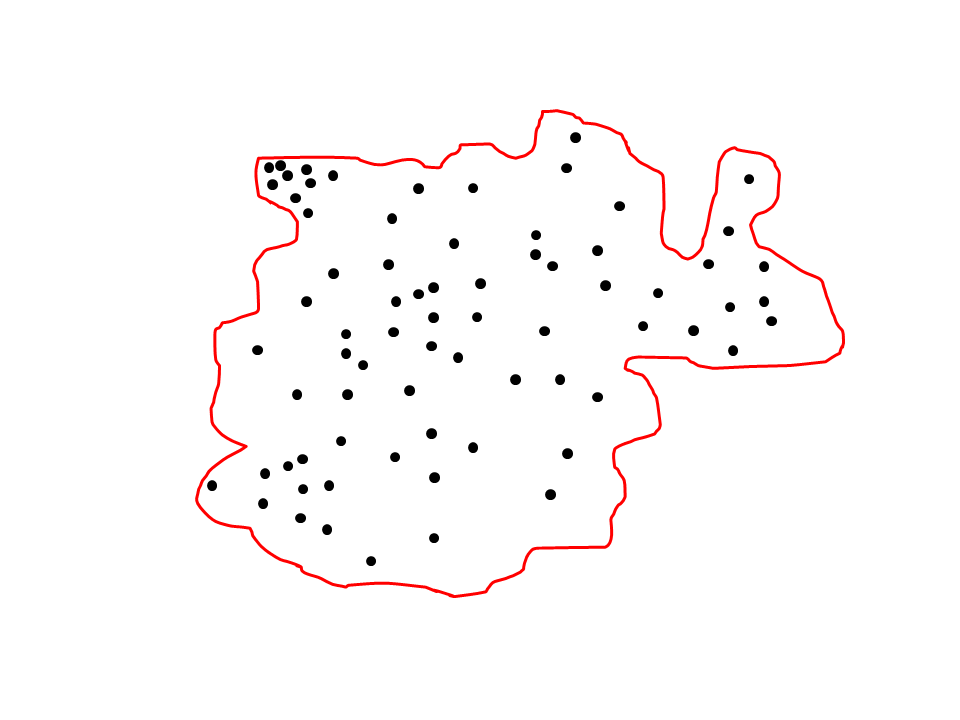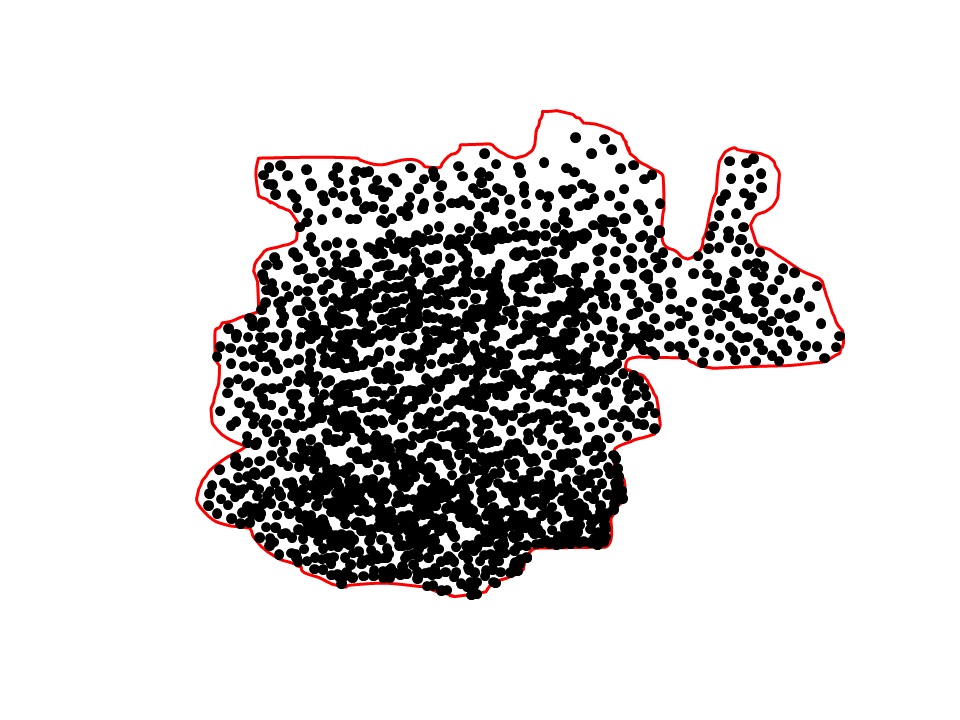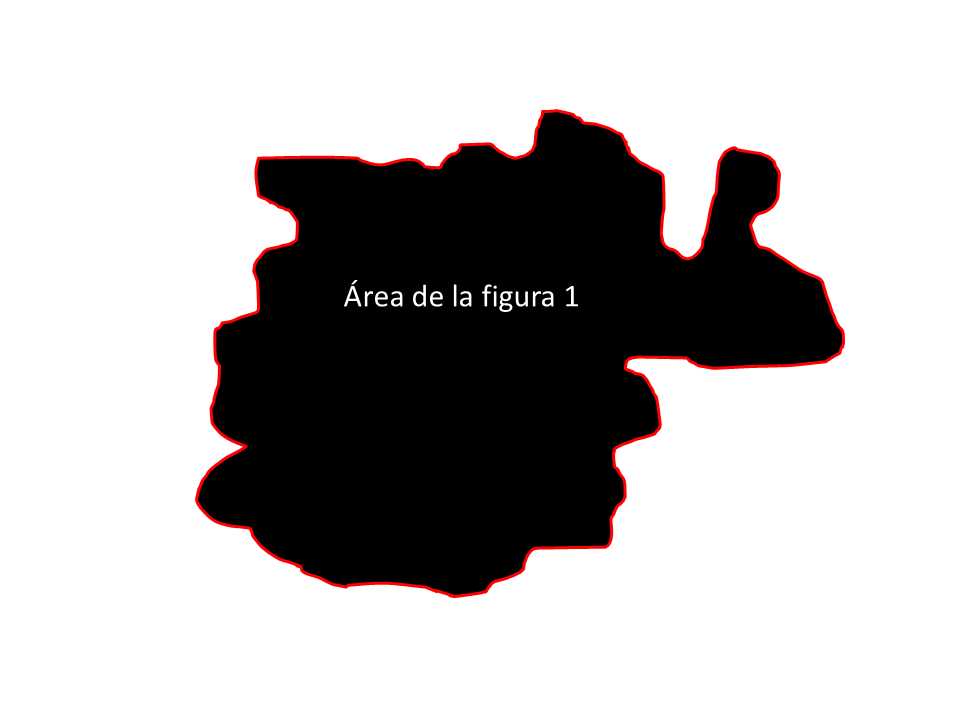
Comenzaré haciendo una figura cerrada cualquiera, es decir, aquella cuyos extremos se unen en un único punto; y dicha figura la llamaremos contorno. Ver figura 1.
.gif)
Figura 1. Figura geométrica cerrada.
Ahora bien, si llenamos con puntos todo el espacio la figura 1 (o espacio interior del contorno) tal y como lo muestra la figura 2, podemos decir entonces que la suma de todos esos puntos es el área de la figura 1.
.gif)
Figura 2. Área de la figura 1 representada por todos los puntos que llenan el espacio interno del contorno .
Para experimentar esto tomamos una cuerda que será nuestro contorno y construimos una figura cerrada, luego para representar los puntos que definirán el área usamos granos de arroz que llenarán todo el espacio interno de la figura. Ver figuras 3a, 3b y 3c. (Podemos usar cualquier tipo de granos u objetos pequeños más o menos uniformes para simular los puntos).
Figura 3a) Construcción del contorno cerrado. 3b) Llenado con arroz del interior del contorno. 3c) Interior del contorno lleno de arroz representado el área.
3. ¿Y qué pasa con el perímetro?
Con respecto al perímetro es muy fácil entenderlo, y para nuestra experiencia éste no es más que la longitud del contorno de la figura, en este caso es la longitud de nuestra cuerda. Ver Figura 4.
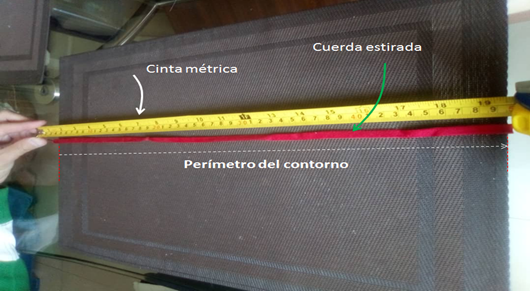
Figura 4. El perímetro del contorno es la longitud de la cuera estirada.
Luego construimos un triángulo con palitos de madera y representamos su área haciendo el mismo procedimiento arriba descrito. Ver Figuras 5a y 5b.
Figura 5a) Llenado con arroz del interior del triángulo. Figura 5b) Área del triángulo representada con arroz.
Para calcular el perímetro del triángulo simplemente sumamos las longitudes de los palitos de madera. Ver figura 6.
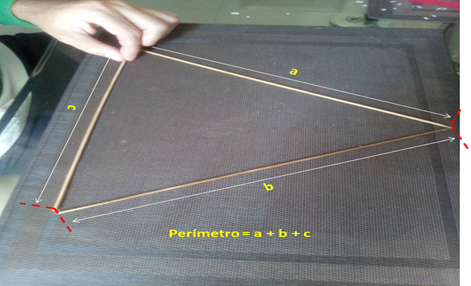
Figura 6. Perímetro del triángulo: suma de las longitudes de los palitos o lados del triángulo.
Con esta experiencia directa el estudiante tiene una noción mucho más real de lo que es el área y el perímetro de una figura geométrica y puede extrapolar estos conceptos a la vida real, como por ejemplo el área de una mesa, de un terreno, etc.
4. Unidades al cuadrado
Todo estudiante de bachillerato sabe que para calcular áreas de figuras geométricas se utilizan fórmulas, por ejemplo para las áreas de los siguientes cuadriláteros usamos las siguientes expresiones matemáticas:
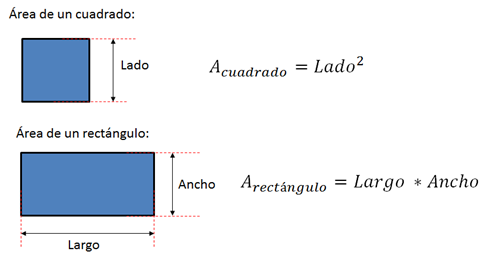
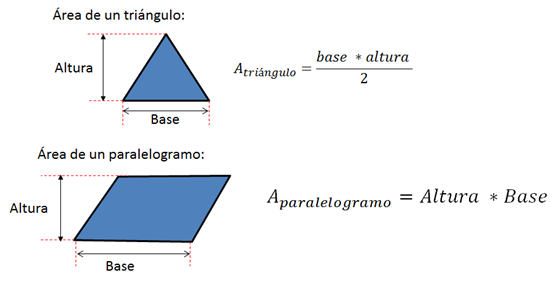
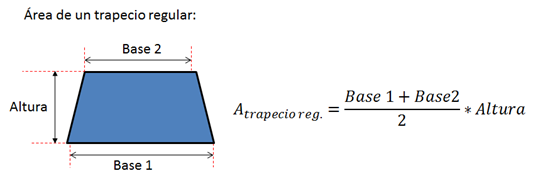
Lo único que se necesita es sustituir los valores de las variables y de esta forma obtenemos el área. Sin embargo, acá vamos a tomar la pregunta que me hizo la estudiante a la que referí al inicio de este artículo: “Si el cuadrado es una figura geométrica de lados iguales, ¿Por qué las áreas vienen dadas en unidades al cuadrado?”
.gif)
Respondamos a esta pregunta de la siguiente forma:
Hallemos el área del siguiente rectángulo usando la fórmula correspondiente
Ese valor del área, que se lee ochenta unidades al cuadrado, quiere decir que el rectángulo tiene un área equivalente a 80 cuadrados cuyos lado miden una unidad de longitud “u”, es decir, que si el resultado fuese 80 cm2 quiere decir que su área es equivalente a 80 cuadrados de 1 cm de lado. Ver figura 7.
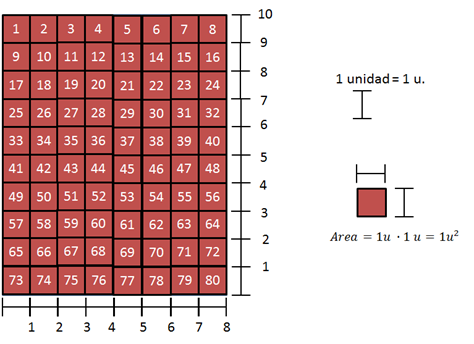
Figura 7. Rectángulo compuesto de 80 cuadrados cuyos lados miden 1 unidad de longitud.
Lo interesante es que esto se aplica a cualquier cuadrilátero, e incluso a cualquier figura geométrica pero esto último requiere de un poco más de matemática.
Pero concentrémonos en los cuadriláteros arriba señalados y vayamos a los experimentos o a lo que yo he llamado laboratorio vivencial casero.
5. Cálculo de áreas. Laboratorio vivencial
Área de un triángulo
Para calcular el área de un triángulo sigamos los siguientes pasos:
a) Dibujemos con regla y escuadra un triángulo cualquiera. Ver Figura 8.
Figura 8. Dibujar un triángulo cualquiera.
b) Definamos un cuadrado cuyo lado mida una unidad de longitud cualquiera, este cuadrado lo usaremos para medir las áreas de los cuadriláteros y lo llamaremos cuadrado unitario. Ver Figura 9.
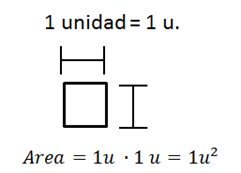
Figura 9. Cuadrado unitario de área igual a una unidad al cuadrado.
c) Encima del triángulo dibujado (Fig. 8), dibujemos una figura que compuesta de cuadrados unitarios de tal forma que el triángulo quede inscrito en dicha figura. Ver Figura 10.
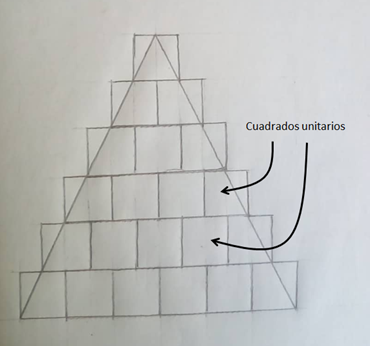
Figura 10. Figura formada por los cuadrados unitarios que inscriben al triángulo.
d) Calculemos ahora el área de ese triángulo usando la fórmula
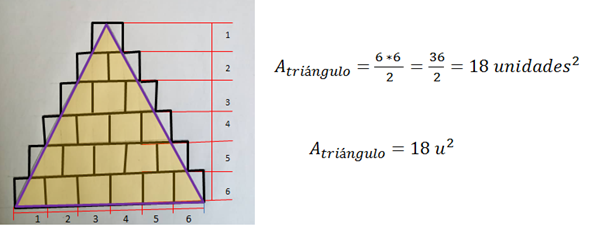
e) Ahora procedemos a recortar el triángulo. Ver figuras 11a y 11b.
Figuras 11a y 11b, recorte del triángulo inscrito.
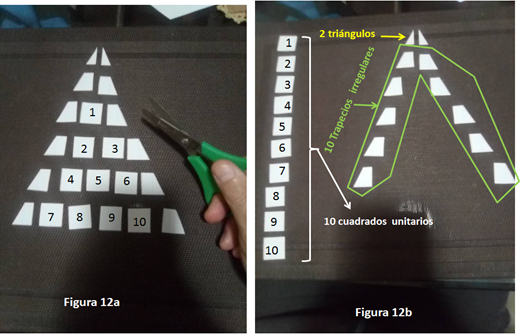
f) Una vez obtenido el triángulo se recortan todas las figuras internas del mismo, de donde obtenemos diez cuadrados unitarios y doce figuras diferentes: dos triángulos y diez trapecios irregulares. Ver figura 12a y 12b.
Figura 12a y 12b Recorte de todas las figuras internas del triángulo se obtienen 10 cuadrados unitarios, 2 triángulos y 10 trapecios regulares.
g) Luego tomamos los trapecios y los cortamos de tal forma que obtenemos diez rectángulos y diez triángulos iguales. Ver figura 13.
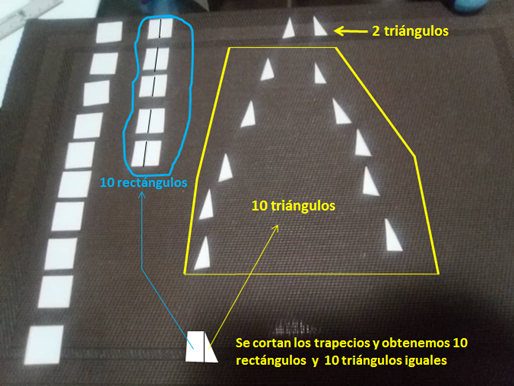
Figura 13. Recorte de los trapecios para obtener 1 rectángulos y 10 triángulos iguales.
h) De tal manera que tenemos las siguientes piezas: 10 cuadrados unitarios, 10 rectángulos y 12 triángulos. Unimos los rectángulos y los triángulos, como si fuera un rompecabezas o puzles, de tal manera que con los 10 rectángulos armamos 5 cuadrados unitarios y con los 12 triángulos 3 cuadrados unitarios para un total de 8 cuadrados. Finalmente tenemos 18 cuadrados unitarios. Ver figura 14.
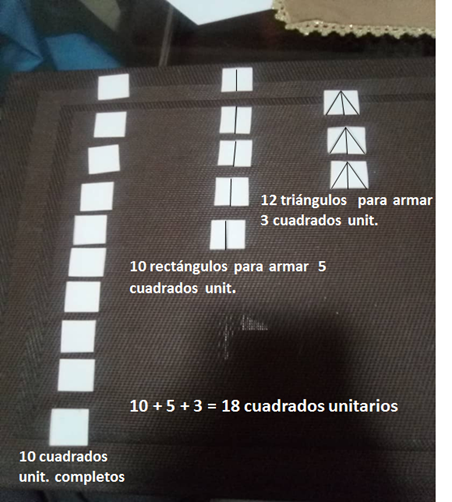
Figura 14. Armado de 8 cuadrados unitarios que sumados a los 10 completos suman 18 cuadrados unitarios.
Como podemos observar hemos obtenido 18 cuadrados unitarios y el cálculo del área del triángulo con el uso de la fórmula es de 18 unidades al cuadrado, es decir, que el área del triángulo es equivalente a sumar todos los cuadrados unitarios que “quepan” en el interior del triángulo.
Esta experiencia la podemos aplicar para el paralelogramo, el trapecio regular y cualquier polígono de n lados, obviamente a medida que aumentamos los lados del polígono el recorte de las figuras (o piezas de nuestro rompecabezas) se hace más complicado.
Cuando la figura tiene trozos de contornos curvos, o es un círculo, la cosa se complica aún más y estaríamos hablando de algo que los matemáticos llaman la cuadratura del círculo, que no es más que hallar un círculo cuya área sea igual a la de un cuadrado, pero esto es otro tema que tocaremos en otra oportunidad.
6. Conclusión
Con este experimento pudimos relacionar las unidades al cuadrado de las áreas con la figura geométrica de un cuadrado. Hemos demostrado por medio de una experiencia vivencial que el área de un triángulo es equivalente al número de cuadrados unitarios que contiene en su interior. Lo hemos hecho recortando figuras de papel con las que obtuvimos varias piezas que con un poco de ingenio o intuición henos armado como un rompecabezas o puzle; las piezas que se armaron son precisamente esos cuadrados unitarios y el número total de ellos nos dio el área del triángulo que obviamente coincidió con el calculado usando la fórmula.
Se ha logrado poner en contacto directo al estudiante con conceptos que parecen existir sólo en nuestra mente; el alumno aprende matemática haciendo cosas con sus propias manos y de esta forma comprende y relaciona dichos conceptos usando objetos reales con los que tenemos una experiencia lúdica y divertida.
Referencias bibliográficas
1.- Baldor J. A. Geometría plana y del espacio. Y trigonometría. Cultural venezolana S.A. Caracas 1986.
2.- Granville W. A., et al. Trigonometría plana y esférica. Limusa.
3.- Lehmann Charles. Geometría analitica. Limusa, México, D.F. 1980.
4.- Irene Rámirez Ana Irene. Geometría analítica : una introducción a la geometría. México : UNAM, Facultad de Ciencias, Coordinación de Servicios Editoriales, 2004.
Saludos estimado Profesor @rnunez
Excelente forma didactica de explicar un tema que muchas veces resulta incomprensible a muchos estudiantes.
Por favor, si puedes indicar algunas referencias sobre este tema quedaría completo para que los lectores recurran a la búsqueda de mayor información.
Gracias por las observaciones realizadas, ya coloqué las fuentes consultadas, seré más cuidadosa la próxima vez.
¡Felicitaciones!
1. Invierte en el PROYECTO ENTROPÍA y recibe ganancias semanalmente. Entra aquí para más información.
3. Suscríbete a nuestra COMUNIDAD, apoya al trail de @Entropia y así podrás ganar recompensas de curación de forma automática. Entra aquí para más información sobre nuestro trail.
4. Creación de cuentas nuevas de Hive aquí.
5. Visita nuestro canal de Youtube.
Atentamente
El equipo de curación del PROYECTO ENTROPÍA
Hola, es una gran explicación y muy didáctica, slds.
Gracias a ti por leer, Saludos
Saludos estimado @rnunez09 un placer saludarlo y leer su contenido, que me pareció muy didáctico y los experimentos realizados están muy acordes a la excelente explicación que realizó, si duda alguna como usted lo indica es un material que no solo es de gran ayuda para estudiantes de bachillerato sino para estudiantes universitarios, en agronomía siempre hablamos que 1 hectárea equivale a un área de 10.000 m2 y aveces los estudiantes tienden a estar un poco confusos al respecto, su material seguro estoy que aclararía muchas interrogantes. Seguimos en comunicación !
Muchísimas Gracias por su comentario. Esto me motiva a seguir haciendo este tipo de publicaciones. Me alegra saber que este trabajo ayude a profesores a complementar sus clases. Una vez más muchísimas gracias
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Please consider using the STEMsocial app app and including @stemsocial as a beneficiary to get a stronger support.
Fantástico, esto buenos recuerdos de mi profesora de matemáticas en bachillerato, ella hacía ver todo muy fácil, siempre buscaba la forma de dar las clases muy didacticas y divertidas para que sus estudiantes pudieran aprender de forma fácil y no vieran la matemática o en este caso la geometría aburrida.
Gracias por esto @rnunez09
Muy buen post hermano @rnunez09. Veo que comienzas a aprender a hacer gifs animados que, como bien sabemos, son una herramienta poderosa para transmitir conocimiento de forma clara. Te felicito. Un cordial saludo.
Saludos @rnunez, excelente forma de iniciar tu post. En el cual, introduces las vivencias diarias y reales. Si bien en un principio pudo ser una pregunta tonta ¡mira! todo lo que género, una gran explicación y aprendizaje por ambas partes.