Saludos estimados lectores de la plataforma Hive. En esta ocasión, como parte del análisis de sistemas isostáticos compartiré un abordaje sobre las Ecuaciones de Equilibrio Estático y su aplicación en la Estática Aplicada y la Ingeniería Civil. En la presente publicación se abordará el uso de estas ecuaciones para hallar incógnitas (reacciones) externas de sistemas isostáticos (de solo una chapa) sometidos a un sistema de cargas externas. Previamente, se abordó el Principio del Trabajo Virtual para Cuerpos Rígidos, el cual es un procedimiento alternativo a las ecuaciones de equilibrio estático para el cálculo de reacciones y además se mencionaron los conceptos de cargas, reacciones, fuerzas puntuales, momentos, solicitaciones, etc.:
•Cálculo de reacciones externas mediante el Principio del Trabajo Virtual para Cuerpos Rígidos

Introducción
En Estática Aplicada, además del análisis de la estabilidad, los teoremas de los polos, los diagramas cartesianos de desplazamiento y el principio del trabajo virtual para el cálculo de reacciones, se estudian en profundidad los sistemas isostáticos, es decir, sistemas que poseen el grado mínimo de estabilidad (no pueden moverse). Los grados de libertad son nulos (GL=0), por lo tanto, el número de incógnitas estáticas (restricciones o unidades de vinculación externas e internas) iguala al número de ecuaciones de condición que se pueden plantear. Esto implica que estos sistemas permiten la aplicación directa de las ecuaciones de equilibrio estático para hallar todas sus incógnitas estáticas. Para garantizar el equilibrio estático de un sistema deben cumplirse ciertas condiciones, además de la condición de poseer el número mínimo de restricciones de movimiento. Primero la sumatoria de fuerzas en cualquier dirección debe ser igual a cero, luego la sumatoria de momentos en cualquier punto debe ser también nula.
Las incógnitas estáticas están representadas por todas las reacciones externas e internas que se generan en el sistema isostático. Las reacciones externas se generan en los vínculos externos o apoyados sobre el sistema tierra (vínculos con líneas diagonales). Generalmente, se suelen hallar todas las reacciones externas para luego mediante un despiece o “desensamble” de todos los elementos del sistema se logren calcular las reacciones internas que se transmiten de un elemento a otro. Si consideramos al mismo tiempo las reacciones tanto externas como internas, el número de incógnitas se elevaría de manera considerable, es por ello que primero determinamos todas las reacciones externas. Sin embargo, en la presente publicación se abordarán sistemas que poseen solo una chapa o cuerpo rígido único, es decir, no existirán vínculos internos en estos y las únicas incógnitas estáticas vienen representadas por las restricciones externas.
Fundamentos Teóricos
En la mayoría de los sistemas estructurales los elementos que soportan cargas pueden representarse en un solo plano o sección, además las cargas aplicadas sobre estos elementos estructurales también suelen encontrarse en este mismo plano. Esto se ve, por ejemplo, en los pórticos (marcos) de un edificio regular, por ello se acostumbra a realizar análisis sobre sistemas bidimensionales. En lo que respecta a estructuras tridimensionales, el cálculo de reacciones no introduce algún principio nuevo, pero incrementa en gran medida la complejidad de los cálculos. Debido a esto se hace más práctico para fines académicos el análisis de sistemas isostáticos planos.
Ya que los grados de libertad son nulos, podemos emplear la siguiente ecuación, extraída del artículo: Determinación Algebraica de los Grados de Libertad de Sistemas Materiales en Estática Aplicada y Ejemplo de Aplicación, la cual es una de las ecuaciones más utilizadas para determinar el grado de estabilidad de sistemas materiales.
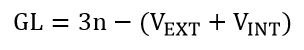
De acuerdo a esta ecuación, donde “n” representa el número de chapas del sistema material, “VEXT” y “VINT” representan el número de unidades de vinculación (restricciones) externas e internas respectivamente, todo sistema isostático debe de poseer el número suficiente de restricciones (unidades de vinculación) para anular todos los grados de libertad que cada chapa posee. Si nos referimos a sistemas planos, en donde las chapas son láminas planas, tenemos que cada chapa de forma individual posee tres (3) grados de libertad (desplazamiento horizontal, desplazamiento vertical y rotación). Por consiguiente, un sistema material compuesto por “n” chapas libres de realizar cualquier movimiento en el plano posee “3n” grados de libertad.
Debe tenerse en cuenta que esta ecuación no incluye o distingue los vínculos aparentes o restricciones redundantes que no aportan estabilidad, por lo que para un análisis más preciso podría verificarse el no cumplimiento de los teoremas de los polos para verificar la no existencia de mecanismos inestables dentro del sistema. Esta no es la única ecuación utilizada para determinar el grado de estabilidad de un sistema material, pero cualquier método o ecuación para verificar que el sistema es isostático estable también son válidos.
Puesto que cada vinculación posee unas unidades de vinculación específicas, de acuerdo al movimiento que esta restrinja, el lector puede encontrar más información sobre los vínculos en Estática Aplicada en el siguiente artículo: Estática Aplicada: los Vínculos y su Aplicación a Sistemas Estructurales en la Realidad.
Para sistemas isostáticos en los que n=1, no existen vínculos internos, por lo tanto, el término “VINT” es nulo. Esto nos deja con la siguiente simplificación:
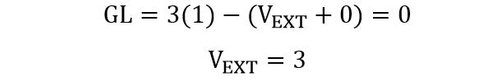
Esto quiere decir que para anular los tres grados de libertad que una chapa en el plano posee, se requieren tres restricciones o unidades de vinculación externas. Las incógnitas estáticas o reacciones a calcular vienen representadas directamente por las restricciones o unidades de vinculación que cada vínculo proporciona. Previamente al uso de las ecuaciones de equilibrio estático, se debe verificar que se cumple la condición de que los grados de libertad son nulos, puesto que, en el caso de sistemas hiperestáticos (donde los grados de libertad resultan ser negativos), existen más restricciones (incógnitas) de las necesarias para que el sistema esté en equilibrio, entonces el número de incógnitas supera al número de ecuaciones que se pueden plantear, resultando que para lograr calcular todas las reacciones, se debe emplear algún método adicional a las ecuaciones de equilibrio estático. El análisis de sistemas hiperestáticos se realiza en las asignaturas que siguen a “Estática Aplicada”. Muchas fuentes caracterizan a los sistemas isostáticos como estáticamente determinados y los hiperestáticos como estáticamente indeterminados, las cuales son otra forma de denominarlos. Si los grados de libertad resultan ser mayores a cero, el sistema es un mecanismo inestable, y al ser capaz de presentar movimiento no puede considerarse isostático ya que ante la aplicación de cargas externas es susceptible de perder el estado de reposo.
Ya que los sistemas isostáticos no pueden moverse (están en reposo), ante la aplicación de un sistema de cargas externo seguirán en reposo (equilibrio estático), por lo que las resultantes de todas las fuerzas y los momentos que actúan en el sistema son nulas. De aquí surgen las ecuaciones fundamentales del equilibrio estático:
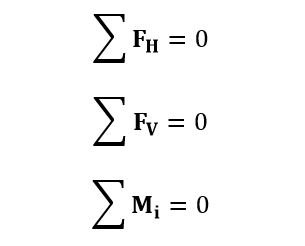
Se tiene que las sumatorias de fuerzas en dirección horizontal (“H”) y vertical (“V”) deben ser nulas, luego la sumatoria de momentos en cualquier punto “i” del sistema debe ser también nula. Dichas ecuaciones son condiciones generales que deben cumplirse en el sistema para garantizar su equilibrio. En el caso de sistemas isostáticos compuestos con varias chapas y vinculaciones internas entre ellas, estas ecuaciones también son aplicables, pero debido a que se tienen más de tres incógnitas externas necesitaríamos hacer uso de las ecuaciones de condición sobre los vínculos internos, esto se abordará en la siguiente publicación.
Ejemplos prácticos
Para el cálculo de las reacciones externas podemos hacer uso de estas tres ecuaciones, por ejemplo, en el caso más básico de sistema isostático: la “viga simplemente apoyada”. En la Fig. N°1 se observa una chapa unidimensional (barra) horizontal simplemente apoyada sometida a una carga distribuida uniforme. Además, se ha realizado un diagrama de cuerpo libre, evidenciando sus reacciones externas.
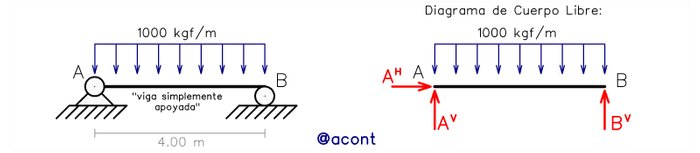
La barra por si sola posee tres (3) grados de libertad, y para que sea isostática, posee tres (3) restricciones externas: las restricciones de desplazamiento horizontal y vertical que proporciona la articulación fija en “A” y la restricción de desplazamiento vertical que proporciona el apoyo simple “rodillo” en “B”. Podemos observar en el diagrama de cuerpo libre que las reacciones externas en “A” concurren en dicho punto, por lo que podemos aprovechar esta situación para plantear allí la sumatoria de momentos (asumiendo el sentido anti horario como positivo), ya que ambas reacciones no tendrían “brazo” para generar momento y la ecuación resultante solo tendría una incógnita a despejar: la reacción vertical de “B” (BV).
Una vez realizado esto, la sumatoria de fuerzas verticales en todo el sistema nos brinda la posibilidad de despejar una sola incógnita desconocida: (AV). Ya que no hay cargas externas actuando en dirección horizontal, resulta evidente que AH será igual a cero.

La carga distribuida posee una fuerza resultante equivalente de magnitud igual a su área actuando en su centro geométrico, por ello el “brazo” de momento de esta es igual a dos metros. Al ser simétrico el sistema de cargas, ambas reacciones verticales resultaron ser iguales.
Cabe destacar un aspecto importante sobre la posición de las reacciones y la estabilidad: si la reacción vertical de “B” fuera horizontal, todas las reacciones del sistema concurrirían en el punto “A”, impidiendo así que exista equilibrio de momentos en dicho punto (la barra podría girar alrededor de “A”). Esto se debe a que si el “rodillo” en “B” se girara 90°, su restricción de desplazamiento en realidad no aportaría estabilidad, ya que sería un vínculo aparente. Lo mismo sucedería si todas las tres reacciones se alinearan, por ejemplo, en dirección vertical, puede que con dos “rodillos” en esta dirección se garantice que la chapa no rote y tampoco se desplace en dirección vertical haciendo que solo haga falta restringir el desplazamiento horizontal, pero agregar un tercer “rodillo” en la misma dirección no aportaría ninguna restricción nueva y este último sería un vínculo aparente. En esta situación, el sistema sería inestable ante la aplicación de cargas horizontales.
Otro ejemplo real básico de sistema isostático sería una “viga en voladizo”, representada por una chapa horizontal con un extremo totalmente restringido de todo movimiento (empotramiento en “A”) y otro extremo libre “B” (Fig. N°2).
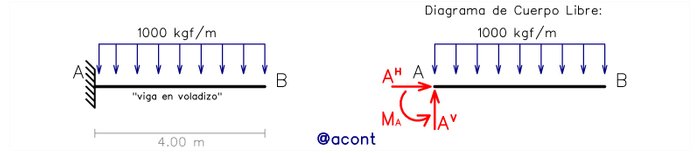
En el diagrama de cuerpo libre se evidencia que todas las reacciones externas se concentran en el empotramiento, ya que este punto no permite ningún movimiento y la restricción del movimiento genera reacciones ante la aplicación de cargas. Las reacciones puntuales AH y AV concurren en el punto “A”, por lo que mediante una sumatoria de momentos en dicho punto se puede hallar el momento MA. Verticalmente solo se observa una incógnita (AV), mientras que horizontalmente sucede lo mismo con AH. Una sumatoria de fuerzas en cada dirección nos permitirá determinar las reacciones puntuales de “A”.
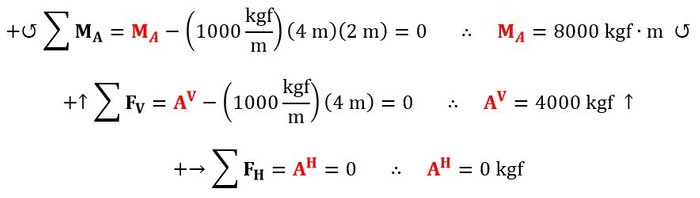
En la próxima publicación se abordarán las ecuaciones de condición para el cálculo de reacciones externas en sistemas isostáticos que poseen más de una chapa, lo cual introduce cierta complejidad dada por el arreglo de chapas y vinculaciones que dichos sistemas pueden poseer.
Aplicaciones de las Ecuaciones de Equilibrio Estático en la Ingeniería Civil
El cálculo de reacciones externas constituye la práctica base fundamental del estudio de la Estática y su uso se extiende hasta las asignaturas más avanzadas del análisis estructural, de allí la importancia de su correcta aplicación para el estudiante de Ingeniería Civil. El cálculo de algunos elementos en estructuras de acero se hace bajo la hipótesis de que están “simplemente apoyados” (Fig. N°3). Las vigas que dan soporte a balcones se pueden modelar de manera similar a la “viga en voladizo”. De igual forma, el cálculo del acero de refuerzo de una zapata para una fundación directa de concreto armado se hace asumiendo que los extremos de esta están “empotrados” a la columna a la que dan soporte.
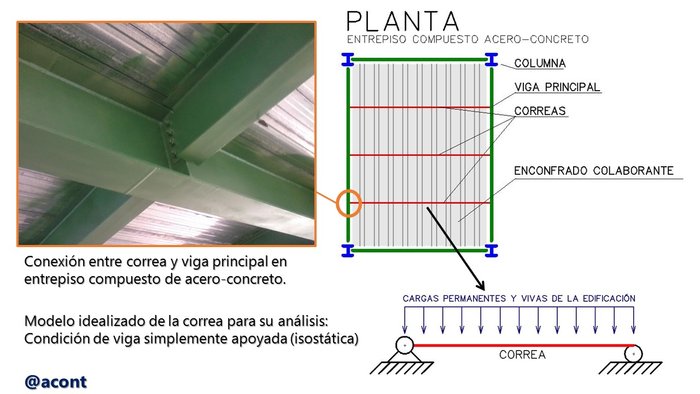
La conexión en acero mostrada en la Figura N°3 se puede modelar como una articulación libre de fricción, ya que la rigidez a flexión o “resistencia al giro” de la misma es relativamente baja respecto a otros tipos de conexiones, y la reacción de momento que se genera allí a causa de las cargas no es significativa. Si bien ambos extremos son iguales ¿Por qué uno de los extremos se modela como apoyo simple y no articulación fija? El modelo de viga isostática permite la aplicación directa de las tres ecuaciones fundamentales, una articulación fija adicional haría que su modelo sea innecesariamente hiperestático. Por otro lado, la mayoría de los elementos estructurales horizontales en una edificación no llegan a estar sometidos a fuerzas axiales (longitudinales) de mayor importancia ya que su función principal es soportar cargas verticales, por lo que la condición de “viga simplemente apoyada” deja en evidencia que se asume la no existencia de fuerzas horizontales.

En la Figura N°4 se observa el modelado de los elementos de un muro de concreto armado en voladizo (“T” invertida). Cada elemento se asume empotrado en un extremo para así formar un cuerpo rígido isostático. El cálculo de las reacciones externas en cada uno de los tres elementos por separado es equivalente al cálculo de las reacciones internas o solicitaciones que actúan en el extremo más desfavorable del muro. La magnitud de estas solicitaciones se utiliza para el diseño del muro, esto implica el dimensionamiento de sus elementos, cantidad de acero de refuerzo, etc. Esta forma de analizar y diseñar el muro nos brinda un enfoque simplificado de cálculo. Si bien el diseño de un muro de contención incluye otros aspectos técnicos y también existen programas computacionales que permiten calcular las fuerzas internas de manera más precisa, sirve de ejemplo para ilustrar el uso de las ecuaciones de equilibrio estático en la Ingeniería Civil.
Conclusiones
Referencias Bibliográficas
[1]Hibbeler, R. C. (2012). Análisis Estructural. Octava Edición. PEARSON EDUCACIÓN, México. (p. 47-48).Fuente
[2]Norris, C. H. y Wilbur, J. B. (1973). Análisis Elemental de Estructuras. Segunda Edición. Libros McGraw-Hill de México. (p. 69, 72-73).Fuente
[3]Rodríguez, Iván. (2003). Estática de las Estructuras. (p. 69-71).Fuente
Material recomendado
•Estática Aplicada: los Vínculos y su Aplicación a Sistemas Estructurales en la Realidad
•Cálculo de reacciones externas mediante el Principio del Trabajo Virtual para Cuerpos Rígidos
Imágenes de autoría propia realizadas mediante LibreCAD y ecuaciones elaboradas mediante Microsoft Word. Figuras N°3 y N°4 elaboradas mediante Microsoft PowerPoint.
Visite la etiqueta #STEM-espanol para encontrar contenido de calidad en habla hispana referente a Ciencias, Tecnología, Ingeniería, Matemáticas y otros tópicos relacionados. @STEM-espanol es una comunidad dedicada a la difusión de contenido en español referente a STEM (ciencia, tecnología, ingeniería y matemáticas por sus siglas en inglés) conformada por autores de todo el mundo.
Para mayor información y si deseas publicar contenido STEM acá está el enlace de invitación al canal de Discord de #STEM-espanol: https://discord.gg/UJwQXWP donde puedes presentarte y aclarar dudas.

STEMsocial es un proyecto en la plataforma Hive al cual #STEM-espanol está adscrito, cuyo objetivo es crear un nuevo paradigma de comunicación STEM en Hive.
Ing. Angel Contreras
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @steemstem account (for some ROI).
Thanks for using the STEMsocial app and including @steemstem as a beneficiaryi, which give you stronger support.