Saludos y bienvenidos estimados lectores de la plataforma Hive, en esta ocasión aprovecho la oportunidad para compartir sobre un procedimiento utilizado en la Estática Aplicada para el cálculo de reacciones externas e internas en sistemas isostáticos (de cero grados de libertad) sometidos a un sistema de cargas externas. Se trata del Principio del Trabajo Virtual para Cuerpos Rígidos (PTVCR).
Todo el contenido sobre Estática Aplicada (1160) se ha recopilado en la siguiente publicación:

Para aplicar eficientemente el PTVCR, es recomendable tener claro cómo realizar los diagramas cartesianos de desplazamiento, puesto que se hará uso de ellos como parte de los procedimientos para el cálculo de reacciones mediante el PTVCR. En publicaciones previas, se abordó este procedimiento gráfico:
•Diagramas cartesianos de desplazamiento y aplicación al principio de los trabajos virtuales (acá se aborda el PTVCR de manera simplificada).
•Diagramas cartesianos de desplazamiento en sistemas materiales de 1 grado de libertad
•Diagramas cartesianos de desplazamiento: uso del diagrama auxiliar
En Estática Aplicada, el Principio del Trabajo Virtual para Cuerpos Rígidos es un tema con diversas aristas, por lo cual, para abarcarlo de manera satisfactoria me gustaría compartir dos publicaciones:
•Parte I: PTVCR, conceptos básicos, fundamentos y aplicación al cálculo de reacciones externas (presente publicación).
•Parte II: abordaje sobre las solicitaciones y aplicación del PTVCR en el cálculo de reacciones internas. (siguiente publicación)
Mediante estos dos artículos compartiré un abordaje teórico-práctico del PTVCR aplicado al cálculo de reacciones, con el objetivo de abordar aspectos que la bibliografía disponible quizás no profundiza lo suficiente como para que sea una referencia amigable hacia estudiantes de Ingeniería. Es por ello que se da la elaboración de este material, para agregar contenido original en el que comparto mis conocimientos como ex preparador (teacher assistant) de Estática Aplicada en conjunto con el uso de una herramienta gráfica y sencilla como lo es LibreCAD, la cual es de gran utilidad para generar figuras y diagramaciones de alta resolución sin la necesidad de utilizar tantos recursos de la computadora, como sería en caso con AutoCAD.
Introducción
Cuando se quieren calcular las reacciones externas e internas en sistemas isostáticos, el uso de las ecuaciones de equilibrio estático (sumatoria de fuerzas y momentos iguales a cero) es la solución usual y ampliamente extendida. Sin embargo, existe otra herramienta que permite realizar esto sin la necesidad de utilizar dichas ecuaciones: el Principio del Trabajo Virtual para Cuerpos Rígidos (PTVCR). El principio del trabajo virtual ha sido utilizado con mayor frecuencia para el cálculo de desplazamientos en sistemas estructurales planos sometidos a cargas externas, no obstante, esto implica que los miembros de dichas estructuras presentarán deformaciones. En Estática Aplicada, se utiliza el principio del trabajo virtual para el cálculo de reacciones (fuerzas y momentos) en sistemas materiales cuyos miembros son cuerpos rígidos (chapas planas).
El PTVCR, tal como lo indica su nombre, consiste en calcular el trabajo que realizan todas las fuerzas y momentos que actúan sobre un sistema virtual el cual viene dado a partir del sistema original y la reacción que se desee calcular. Dicho sistema virtual no es más que el mismo sistema original solo que con un grado de libertad adicional, es decir, si el sistema original es isostático (cero grados de libertad), el sistema virtual siempre poseerá un (1) grado de libertad. Dicho sistema virtual representa entonces un mecanismo cinemático cuyos desplazamientos (desplazamientos virtuales) deben ser determinados, para así calcular el trabajo virtual que realizan todas las fuerzas y momentos que actúan sobre el sistema original. Es por eso que el uso de los Diagramas Cartesianos de Desplazamiento se hace necesario.
Cabe destacar que el PTVCR permite el cálculo de solo una reacción incógnita a la vez, de manera que deberán realizarse los Diagramas Cartesianos de Desplazamiento tantas veces como reacciones diferentes del sistema se quieran calcular. En comparación a las ecuaciones de equilibrio estático, el uso del PTVCR es poco práctico si se desean calcular todas las reacciones de un sistema isostático, pero si solo se desean calcular dos o tres reacciones incógnitas específicas del sistema, el PTVCR presenta notables ventajas, puesto que no se requiere conocer previamente el valor de otras reacciones incógnita, como puede ser el caso mediante el uso de ecuaciones de equilibrio estático.
Conceptos básicos
Para una mejor comprensión de los procedimientos empleados más adelante, vamos a abordar los siguientes conceptos.
Fundamentos del Principio del Trabajo Virtual para Cuerpos Rígidos
El principio de los trabajos virtuales para cuerpos rígidos fue desarrollado originalmente por John Bernoulli en el año 1717 y se expresa así: ”Si sobre un cuerpo rígido actúa un sistema de cargas externas en equilibrio, el trabajo realizado por dichas cargas cuando el cuerpo sufre un desplazamiento virtual es igual a cero”. El término virtual se refiere específicamente al hecho de que los desplazamientos virtuales no son producidos por las cargas externas que actúan sobre el cuerpo rígido. Estos desplazamientos virtuales son independientes de las cargas externas aplicadas al sistema y el origen de estos se detallará más adelante.
Cuando hablamos de sistemas isostáticos, nos referimos a un conjunto de cuerpos rígidos (chapas) unidos entre sí mediante diferentes condiciones de vinculación, de tal manera que la estabilidad se alcanza mediante el número mínimo de unidades de vinculación que logran restringir totalmente los movimientos en el sistema. Las unidades de vinculación o restricciones representan de manera directa e unívoca a las reacciones incógnitas del sistema, es decir, tanto a las reacciones externas como internas del sistema isostático. Sin embargo, a modo de simplificación, por ahora solo trataremos con las reacciones externas dejando el cálculo de las reacciones internas para la siguiente publicación.
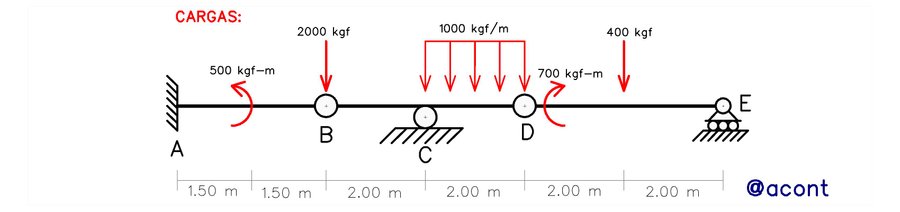
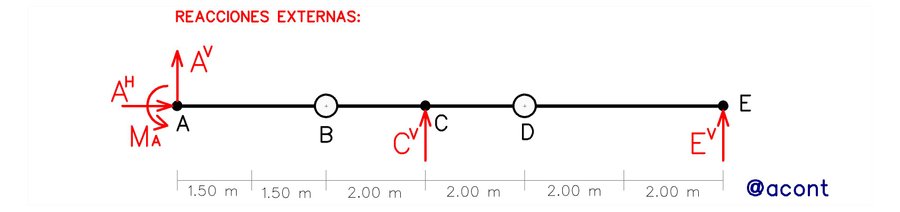
Se puede decir entonces que las reacciones son el producto de la restricción del movimiento en un punto específico del sistema, el cual intenta moverse debido a la aplicación de cargas externas. En la Fig. N°5 podemos observar un sistema isostático donde se han evidenciado sus unidades de vinculación o restricciones en los apoyos a tierra, o de manera equivalente, sus reacciones externas.
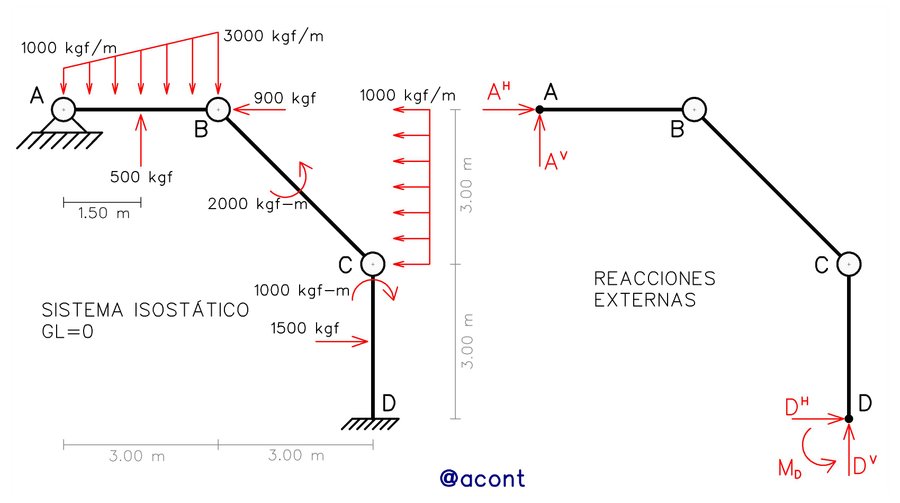
Entonces para aplicar el PTVCR a un sistema isostático, debemos hallar la manera de “darle movimiento” al sistema, de manera que sea capaz de experimentar “desplazamientos virtuales”.
Del sistema mostrado en la Fig. N°5, podemos tomar como nuestra reacción incógnita a calcular a la reacción horizontal del vínculo “D”. En este sentido, podemos asumir que la reacción incógnita de interés se convierte en una carga externa del sistema y deja de ser una restricción como tal del mismo. Esto nos introduce una modificación en el vínculo donde se encuentra la reacción incógnita, de manera que pierde una de sus restricciones. Esto da como resultado que el sistema pierde una (1) restricción o unidad de vinculación, pasando así de tener cero (0) grados de libertad a tener un (1) grado de libertad (mecanismo cinemático). En la Fig. N°6 se ilustra el proceso en el que se modifica la vinculación en donde se encuentra la reacción incógnita.
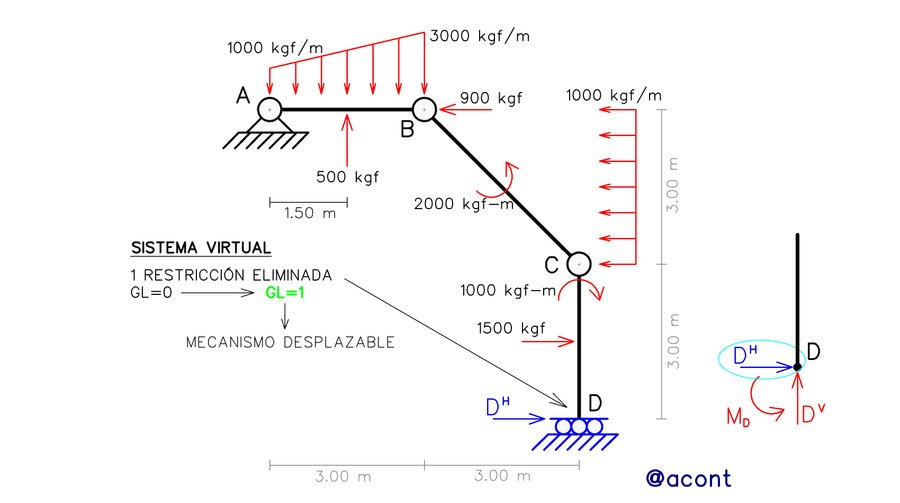
Este mecanismo cinemático de un (1) grado de libertad representa el “sistema virtual” el cual será capaz de presentar desplazamientos virtuales. Estos desplazamientos virtuales son el producto de asumir que el sistema original se convierte en un “mecanismo virtual equivalente” en el cual la reacción incógnita pasa de ser una restricción a ser una carga externa adicional aplicada al sistema isostático. En consecuencia, con el objetivo de calcular el trabajo virtual que realizan todas las cargas aplicadas sobre el sistema, se realizan los Diagramas Cartesianos de Desplazamiento del sistema virtual para así hallar la magnitud de los desplazamientos virtuales (Fig. N°7).
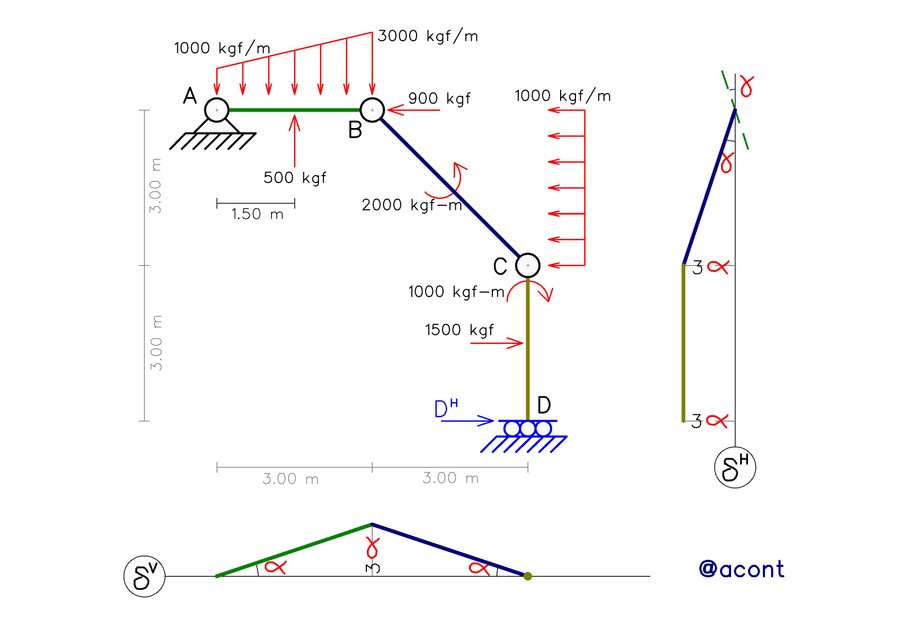
No debemos olvidar que hasta ahora tenemos dos sistemas: el sistema original isostático (que no se mueve) y el sistema virtual (mecanismo de un (1) grado de libertad al cual se le realizaron los Diagramas Cartesianos), sobre ambos actúa el mismo sistema de cargas externas. Ahora, entra en juego el cálculo del trabajo virtual que realizan dichas cargas externas.
Trabajo realizado por un sistema de cargas externo
El trabajo realizado por una fuerza puntual es simplemente el producto escalar de ella por el desplazamiento que se da en su punto de aplicación en dirección a dicha fuerza. Esto implica que, si una fuerza puntual en dirección vertical se encuentra aplicada sobre un punto que presenta desplazamiento únicamente en dirección horizontal, el trabajo realizado por dicha fuerza es nulo ya que el desplazamiento y la fuerza son perpendiculares. Con respecto a los signos del trabajo virtual, podemos simplemente establecer que el trabajo será positivo si la fuerza puntual y el desplazamiento se dan en el mismo sentido y negativo si poseen sentido opuesto. Lo anterior se cumple independientemente del sentido que tenga cada vector por separado y proviene del hecho que en operaciones con vectores el producto escalar viene acompañado por el coseno del ángulo entre ambos.
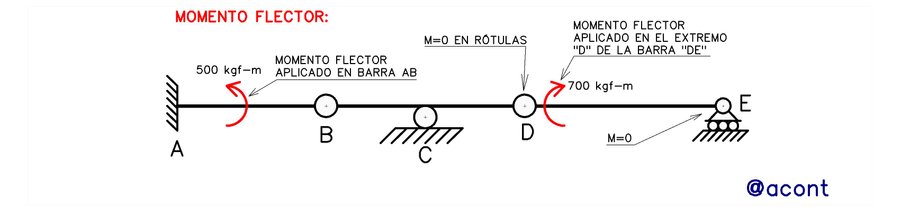
El trabajo realizado por un momento es el producto de su magnitud por la magnitud del ángulo de rotación de la chapa sobre la cual el momento está aplicado. Esta rotación se halla en los diagramas cartesianos de desplazamiento. El signo del trabajo virtual para los momentos se halla de manera similar con la fuerza puntual: si el momento y la chapa rotan en el mismo sentido el trabajo será positivo, y si giran en sentido opuesto será negativo. De lo anterior surge que, si una chapa sufre traslación pura, el trabajo realizado por un momento aplicado sobre la misma será nulo. Cabe destacar que los momentos nunca actuarán puntualmente sobre una rótula o cualquier vinculación cuya rotación no esté restringida, pero si pueden actuar en el extremo de una barra y la rotación de dicha barra o chapa será la que se tomará en cuenta para el cálculo del trabajo virtual.
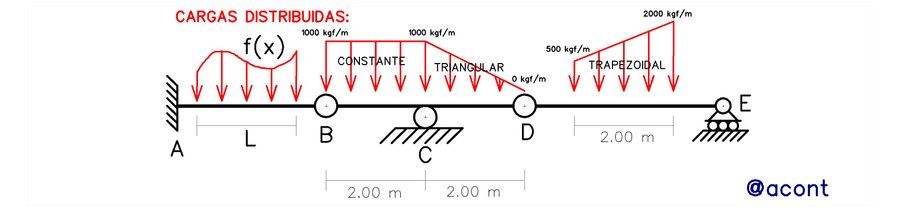
Para el caso de las cargas distribuidas, el trabajo virtual se calculará como el producto de su fuerza resultante por el desplazamiento virtual dado en el punto donde se aplica dicha fuerza resultante. La fuerza resultante de una carga distribuida es simplemente su área, es decir, si la carga distribuida es uniforme, la fuerza resultante es el producto de su valor por la longitud lineal sobre la cual dicha carga se aplica. Si la carga es trapezoidal o triangular se calculará la fuerza resultante (área) de acuerdo a la forma de dichas figuras geométricas, ya que los valores mínimo y máximo de dichas cargas, así como la longitud donde se aplican son conocidas. La fuerza resultante se ubica en el centro de gravedad de la carga distribuida, el cual varía dependiendo de la forma geométrica de la misma (rectangular, triangular o trapezoidal). Como recomendación, se debe procurar separar las cargas trapezoidales en una carga uniforme más una carga triangular, simplificando así el cálculo del centro geométrico.
Podemos generalizar el cálculo del trabajo virtual realizado por un sistema de cargas externo mediante la siguiente ecuación, en donde la sumatoria de todos los trabajos virtuales se expresa como la sumatoria de los trabajos realizados por todas las fuerzas puntuales y momentos sobre el sistema virtual:
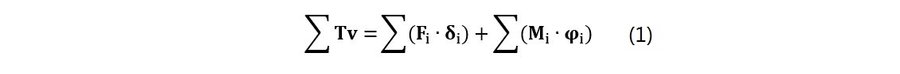.jpg)
Donde el término “Fi” se refiere a las cargas concentradas (fuerzas puntuales) externas, “δi” son los desplazamientos virtuales en dirección a la fuerza puntual en su punto de aplicación, “Mi” son los momentos externos y “φi” son las rotaciones virtuales de la chapa donde el momento se aplica. En la Fig. N°8 se han calculado las fuerzas resultantes para cada carga distribuida y el desplazamiento virtual correspondiente a cada carga externa aplicada al sistema virtual.
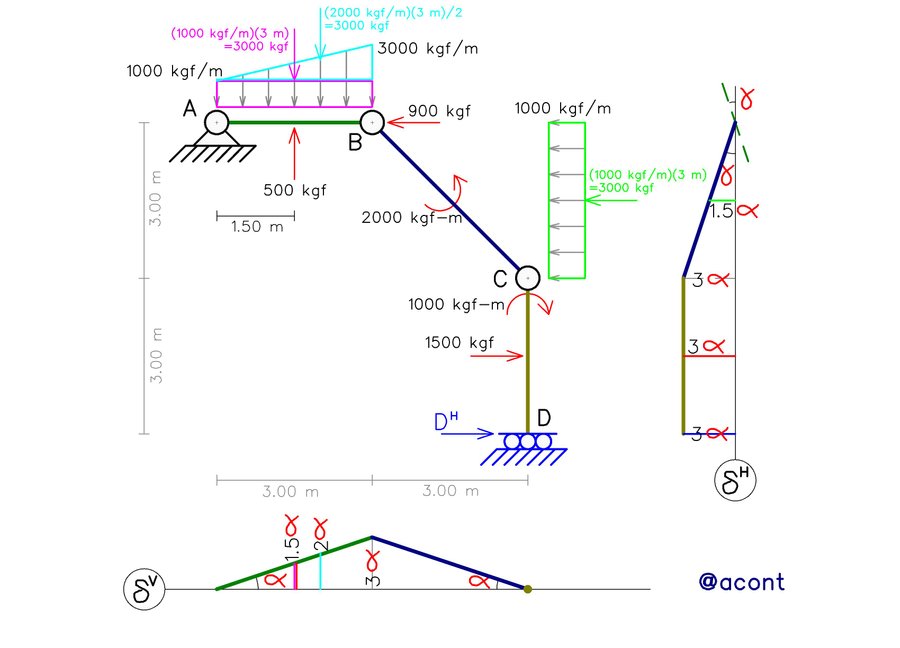
Posteriormente, realizamos la sumatoria de todos los trabajos virtuales según la Fig. N°8, aplicando la ecuación (1):

Podemos notar que el momento de 1000 kgf-m no realiza trabajo porque la chapa en donde se aplica no rota y la fuerza puntual horizontal de 900 kgf tampoco, porque el punto donde se aplica se desplaza en dirección vertical. En caso de presentarse, las fuerzas puntuales inclinadas deben descomponerse en sus componentes horizontal y vertical. Pero esta sumatoria de trabajos virtuales que el sistema de cargas externas realiza sobre el sistema virtual debe de tener cierta relación con el sistema original con el fin de que exista cierta compatibilidad entre ambos sistemas.
Compatibilidad con el sistema original
Con el fin de compatibilizar ambos sistemas, utilizaremos la definición del Principio de los Trabajos Virtuales para Cuerpos Rígidos dada por Bernoulli, en donde el trabajo realizado por el sistema de cargas externo es igual a cero cuando el sistema sufre un desplazamiento virtual. Es decir, si queremos compatibilizar el sistema virtual con el sistema original, debemos igualar a cero la sumatoria de los trabajos virtuales, puesto que el sistema original no se mueve, y el objetivo de esta compatibilidad es hallar el valor de la reacción incógnita que hace que el trabajo sea nulo en el sistema virtual, en otras palabras, hallar el valor de esta incógnita que le da “equilibrio” a este sistema virtual. De esta manera, obtenemos la ecuación fundamental del PTVCR:
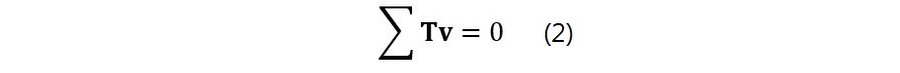.jpg)
El producto de esta compatibilización, utilizando la ecuaciones (1) y (2), es una expresión igualada a cero, en donde el parámetro “
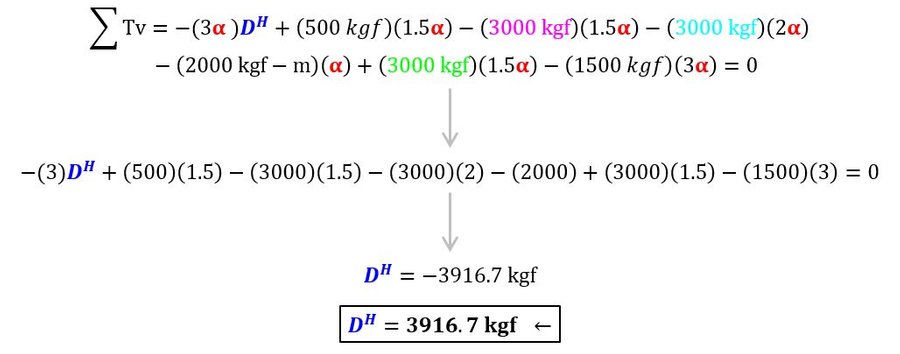
Este es el procedimiento a aplicar para cada reacción que se desee calcular en el sistema isostático. La complejidad en la realización de los diagramas cartesianos depende de que reacción seleccionemos para aplicar el PTVCR ya que el movimiento del sistema virtual depende de que restricción eliminemos en el sistema original, haciendo que en ocasiones una gran porción del sistema virtual no se mueva, simplificando en gran medida el cálculo del PTVCR (ya que hay menos desplazamientos virtuales y más trabajos nulos). El caso con mayor cantidad de trabajos virtuales resulta cuando la eliminación de una restricción en el sistema original genera movimiento en la totalidad del sistema virtual.
En casos especiales deberá hacerse uso del diagrama auxiliar para poder realizar por completo los Diagramas Cartesianos de Desplazamiento. Estos casos se dan cuando dos chapas vinculadas mediante bielas paralelas presentan traslación pura.
De esto se trata el PTVCR para el cálculo de reacciones externas. Quizás lo menos evidente en todo esto es seleccionar la vinculación correcta al eliminar una reacción en la vinculación original puesto que la ejecución del trabajo virtual se logra dominar luego de algo de práctica, por ello compartiré el siguiente contenido, en adición al abordaje teórico-práctico sobre el PTVCR ya realizado.
Análisis de vinculaciones externas. Sistema global.
Ya que la “transformación” que sufre una vinculación externa producto de la eliminación de una de sus restricciones puede no resultar evidente en algunos casos, la elaboración de un material de referencia que brinde un esquema “estandarizado” es de gran ayuda para la realización del PTVCR en el cálculo de reacciones externas. Para ello, debemos repasar un poco las condiciones de restricción dadas por los vínculos externos. En el artículo Estática Aplicada: los Vínculos y su Aplicación a Sistemas Estructurales en la Realidad se puede encontrar más información respecto a las vinculaciones en Estática Aplicada.
Podemos asumir un “sistema de referencia global” para las reacciones externas conformado por un eje horizontal, un eje vertical y un momento en sentido anti horario, todos aplicados en un vínculo externo cualquiera (Fig. N°9).
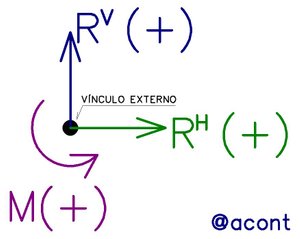
Tenemos que los vínculos externos de 3° grado (empotramiento fijo) restringen todo desplazamiento y a la vez restringen la rotación (no permite ningún movimiento) por lo tanto, la imposibilidad de todo movimiento genera todas las reacciones del sistema global.
Los vínculos externos de 2° grado poseen dos de las tres reacciones del sistema global. La articulación fija solo permite la rotación, por lo que esta vinculación genera ambas fuerzas puntuales del sistema global. El empotramiento móvil, por otro lado, solo permite un desplazamiento, generando la reacción de momento y una de las fuerzas del sistema global.
Los vínculos externos de 1° grado solo generan una de las tres reacciones del sistema global. El ”rodillo” y el “patín” o articulación móvil (apoyos simples) solo generan una fuerza puntual como reacción externa. Mientras que el empotramiento libre solo restringe la rotación, por lo que genera una única reacción externa: el momento.
Se hace notar que una vinculación posee tantas reacciones como grado posee, y que al aplicar el PTVCR, independientemente de qué reacción calculemos, la vinculación a modificar pasará de un grado superior a un grado inmediatamente inferior (de 3° a 2° grado, de 2° a 1° grado o de 1° grado a un punto libre de vinculación).
El análisis del sistema global de reacciones externas de la vinculación a modificar consiste en identificar primero cuáles son las reacciones que dicha vinculación posee, eliminar la restricción asociada a la reacción externa que queremos calcular y luego identificar cuál sería la vinculación correcta a utilizar de acuerdo a las restricciones restantes. Tomando en cuenta las tres restricciones del “sistema global”, podemos encontrar diversas situaciones de acuerdo a las restricciones del vínculo original. En la Tabla N°1 se tiene un resumen de todos los casos que podrían presentarse durante la sustitución del vínculo original por un vínculo virtual de acuerdo a la reacción externa que se desee calcular.
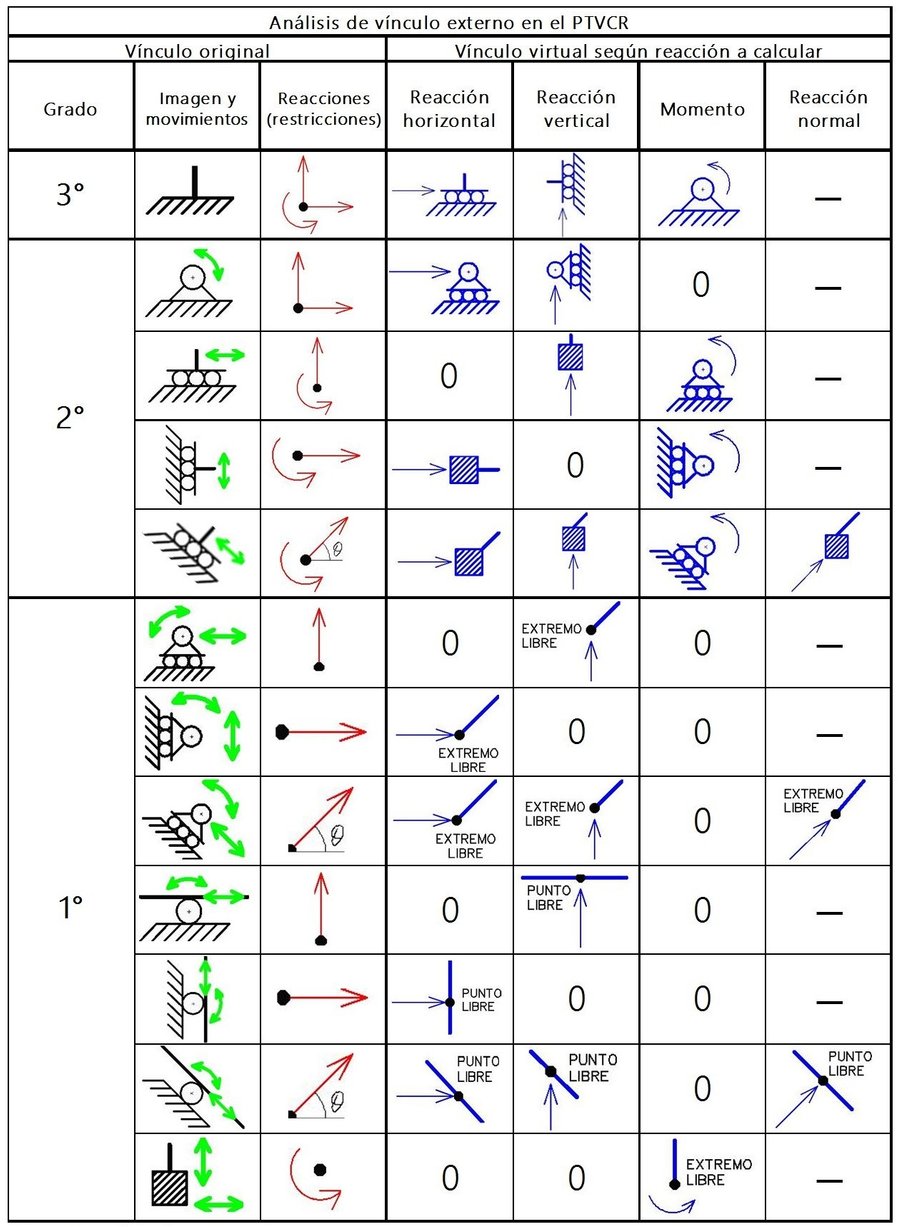
Un error común en muchos estudiantes a la hora de abordar el PTVCR, se da a la hora de elegir la vinculación a utilizar en sustitución de la vinculación original para la ejecución del trabajo virtual, por ello se da la elaboración de esta tabla, sin embargo, a la hora de utilizarla no se debe dejar a un lado el análisis que hay detrás para así corroborar y entender mejor lo que esta tabla expresa. Puede que algunos de los casos dados en la tabla sean muy poco frecuentes o algunos de los vínculos realmente no tengan aplicación alguna en estructuras de la realidad, pero ¿Por qué no cubrir todos los casos que teóricamente se pueden dar y no conformarnos con los vínculos más usuales? Quizás las estructuras civiles del futuro o algún mecanismo novedoso requieran de una vinculación tipo “empotramiento libre” o cualquier otro vínculo poco usual para su modelado, análisis y/o funcionamiento.
Conclusiones
Referencias Bibliográficas
[1]Hernández, Suilio. (1998). Estática Aplicada. Folleto Editado por el Departamento de Ingeniería Estructural U.C.V. Caracas. (p. 55-60).Fuente
[2]Luchsinger, Cecilio. (1976). Estructuras (Volumen I). Folleto de Estructuras N°4. Departamento de Ingeniería Estructural U.C.V. Caracas. (pág. 32)Fuente
[3]Rodríguez, Iván. (2003). Estática de las Estructuras. (p. 69-71, 75-82).Fuente
[4]Serway, Raymond A. y Jewett, John W. (2004). Física para Ciencias e Ingeniería. Volumen I. Séptima edición. Editorial Cengage Learning. (pág. 165).Fuente
Material recomendado
•Diagramas cartesianos de desplazamiento y aplicación al principio de los trabajos virtuales
•Diagramas cartesianos de desplazamiento en sistemas materiales de 1 grado de libertad
•Diagramas cartesianos de desplazamiento: uso del diagrama auxiliar
Imágenes y ecuaciones de autoría propia realizadas mediante LibreCAD y Microsoft Word. Tabla elaborada mediante Microsoft Excel.
Visite la etiqueta #STEM-espanol para encontrar contenido de calidad en habla hispana referente a Ciencias, Tecnología, Ingeniería, Matemáticas y otros tópicos relacionados. @STEM-espanol es una comunidad dedicada a la difusión de contenido en español referente a STEM (ciencia, tecnología, ingeniería y matemáticas por sus siglas en inglés) conformada por autores de todo el mundo.
Para mayor información y si deseas publicar contenido STEM acá está el enlace de invitación al canal de Discord de #STEM-espanol: https://discord.gg/UJwQXWP donde puedes presentarte y aclarar dudas.

STEMsocial es un proyecto en la plataforma Hive al cual #STEM-espanol está adscrito, cuyo objetivo es implementar un medio de comunicación STEM en Hive.
Ing. Angel Contreras
Respuestas a las demás reacciones externas del ejercicio resuelto!
AV=2250 kgf ↑
AH=6316,7 kgf →
DV=3250 kgf ↑
MD=10500 kgf-m ↺
If you appreciate the work we are doing, then consider supporting our witness @stem.witness. Additional witness support to the curie witness would be appreciated as well.
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Thanks for having used the stem.openhive.network app and included @steemstem in the list of beneficiaries of this post. This granted you a stronger support.