Hello friends... @dexterdev is back with his new article. This one is not about coarse-grained simulations. For the past few days I was thinking about active matter systems, non-equilibrium statistical mechanics and irreversibility in the systems etc. And I want to share my excitement about what I learned recently. This article will try to give you an idea about irreversibility in systems which are operating far away from equilibrium.
Active matter is always a dear topic to me. As some of you might know that I was an electronics engineering student in past and most of the magic in electronics are done by active systems like amplifiers, digital switches, and more complicated circuits like microprocessors etc, which make use of the concept called feedback mechanism. Now I realize that all systems including "active" electronics circuits fall in the category of non-equilibrium systems. Some of the attempts to understand these systems are by perturbing them and studying their responses. They call it Linear response theory in Physics. Engineers always do this kind of analysis to understand circuits or other systems. But I am pretty sure that most students in engineering are unaware of the fact that they are dealing with non-equilibrium systems(when dealing with say Amplifiers). One reason for this situation is that Statistical Mechanics is not taught in engineering disciplines(at least in India when I was a student). But the good thing is that we learn Information Theory. This is something most physics students miss in their course work I feel. So the fact is that most of the students in engineering and physics go through many concepts without knowing(or appreciating) their equivalence and primarily this is due to the language barrier in both streams.
A quick introduction to Equilibrium and Non-equilibrium systems
Coming back to the topic now. Let me attempt to give a very short introduction to equilibrium and non-equilibrium systems. I will start with the figure below:
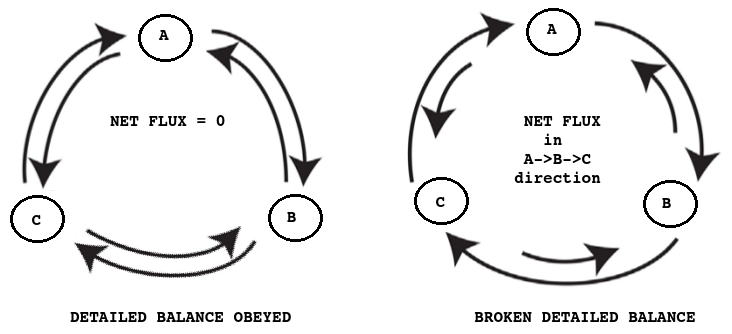
Equilibrium systems obey detailed balance. Non-equilibrium active systems break the detailed balance. Figure by @dexterdev
Let us assume three states A, B and C, represented as in the above figure. It can be outcome of some experiments or any other observations like weather or so. Let us assume the states switches between each other. See the figure in left side. A can go to B and C. Similarly B and C can also move to other states. The length of arrow determines the rate or probability by which this switching happens. In the first case of above figure it can be seen that there is no net flux. C can go to A and A can go to B and in the respective reverse directions. This system is said to be in equilibrium and obeys detailed balance. Now let us see the figure in the right. A can switch to B and B to C in a higher rate than C to B to A(see the length of the arrows which represents the rate of switching). This simply means that there is an asymmetry in the system. Flow in one direction(A->B->C) is preferred over the other. And this is described as a net flow in the system. In the second case, detailed balance is not obeyed and such systems are in non-equilibrium. Some examples are driven systems(they utilize energy to run) like in biology. Some famous examples of non-equilibrium systems are reaction-diffusion systems and patterns arising from such experiments are very interesting ones. I have written few articles in past about modelling reaction-diffusion systems. I suggest this video as a starting point for those who are interested in reaction-diffusion systems:
Kullback-Leibler Divergence
I was equally excited and disturbed after watching a KITP webinar on Nonequilibrium thermodynamics for active matter by Jordan Horowitz(Michigan) and Nikta Fakhri(MIT) as a part of their Symmetry, Thermodynamics and Topology in Active Matter program. Thanks to this tweet by Dr. Shashi(NCBS and ICTS) which came in my feed:
The reason for excitement was to know about a measure which can be used to quantify the irreversibility from the time trajectories. This measure has roots in Information theory and is called Kullback-Leibler divergence(KL divergence or KLD or DKL). KL divergence is a measure to quantify how different two probability distributions(say P and Q) are. It is defined for discrete cases as:

But there is a caveat. This measure is not symmetric. DKL(P||Q) is not equal to DKL(Q||P) ! In Information theoretic view point, KLD is a measure which quantifies the lost information when we approximate a distribution(P) with another one(Q). Those who need an intuitive understanding of KL divergence are advised to have a look at this article[0].
My confusion
In one of the slides in the presentation they takes a forward trajectory and reflects it in time axis to get the reverse trajectory and says the distributions of forward and reverse trajectories are different and can be quantified using KLD! This way of explanation didn't satisfy me and I was disturbed. Maybe I am missing some point. Why would the statistics of reflected trajectory be different from that of the real trajectory? It seems that the trajectories are not forward and reflected ones, but some kind of residual trajectories from them obtained via some "whitening" process[1]. If someone can find a good explanation, let me know it. But this made me to think more on the topic and I started to search for literature in the field. Basically I was looking for something like a toy model to understand this concept properly. And I think I have a fairly good idea about the basics now. And the articles which helped me most are the Ph.D. theses of Momčilo Gavrilov[2] and Édgar Roldán[3].
By the way, I have shared my confusion as a physics.stackexchange question. It would be nice if someone wants to answer it. :)
Irreversibility!
Irreversibility is a feature of living systems, active computer circuits, and many other systems. It is commonly seen in systems which operate far away from equilibrium. These systems exhibit hysteresis, since the forward and reverse trajectories may be completely in different paths. One famous example is the RNA/DNA pulling experiment. See below:
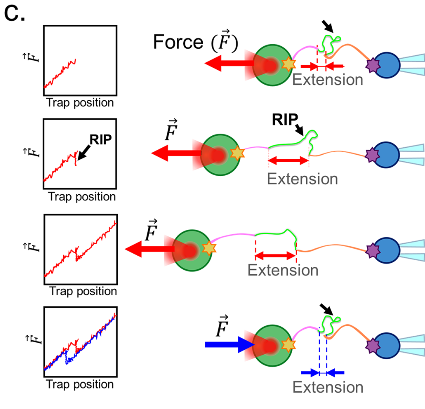
See the trajectories while pulling(forward trajectory: RED) and relaxing(reverse trajectory: BLUE) the polymer. They follow different paths which means this system exhibits "hysteresis". Hysteresis is a feature of systems with memory. A famous example is hard-disk. Image taken from Nathalie Casanova-Morales et al[4], License: CC-BY-4.0
Another experiment which I would like to draw your attention is the memory erasure experiment[2]. Think about a digital flip-flop(or a digital register) where you can store bits of data. Let us take the most simple case. 1 bit memory! It can store either 0 or 1. Once you erase it to 0, you cannot guess what was the bit value you erased. This is a very simple case of irreversibility. So our hypothetical 1 bit memory element can have 2 states, which can be represented as a double-well potential:
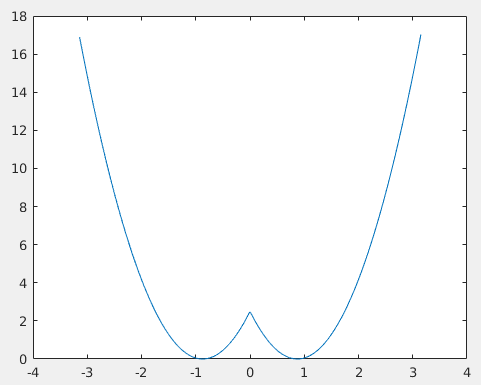
The two minima represents the two states 0 and 1 in the memory element. The Y-axis can be thought of as potential energy. Picture courtesy: @dexterdev
Once you are ready with this double-well potential, we can now proceed with an ensemble of experiments. The experiment consists allowing an imaginary particle to occupy any of these 2 states(any of these 2 wells in the potential). Now we introduce a parameter lambda which changes the shape of the potential function. The operations can be:
- a change in the depth of the wells
- width of the wells
- tilt in the function
The operation on the potential function can be thought as an external field applied to it, which changes its analytical form step by step. The starting point is a symmetrical double well. See the below figure:
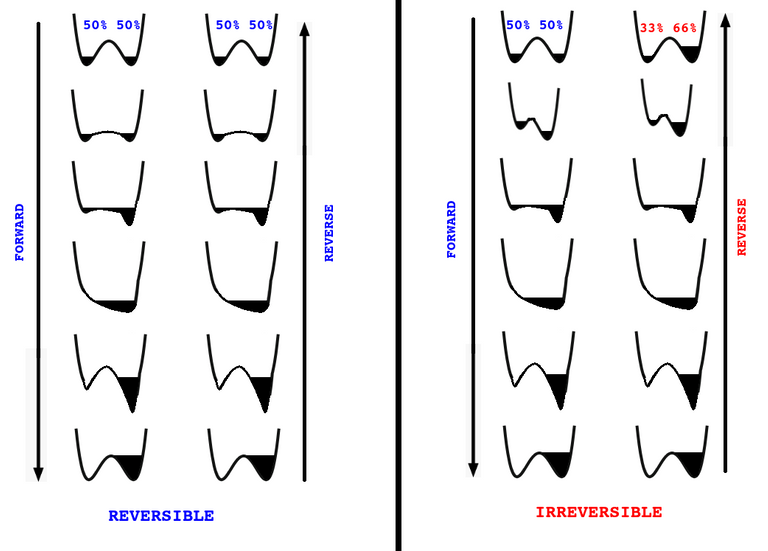
Toy example of memory erasure illustrating reversibility(1st case;left) and irreversibility(2nd case;right) in two different protocols for evolving the potential functions. The only difference in both protocols is in the shape of potential in the second row of the second case(right). The above figure is adapted from reference [2] by me.
I try to think the above experiment in the following way: You have got a particle in any of these wells to start from. Either you start from left or right well(50% chance to be in any of these). Now see how the potential changing its shape in time. Our imaginary particle will try to find a local minima statistically. This experiment is repeated "tonnes" of time to get an ensemble of trajectories. Once the forward experiment is done we repeat it in the reverse direction. In the above figure, you will notice an asymmetry in the second case. The distribution of particles in the beginning and the final distribution in reverse case result doesn't match! This is an example for the irreversibility in the non-equilibrium systems. And in this case the shape of the potential in second row is the reason which gives rise to this asymmetry. The above example shows two different implementations of a 1 bit memory erasure experiment. This asymmetry can be proved analytically by the way. My primary aim was to simplify the concept.
Using KL divergence measure, let us analyze the above results.

Let us see the reversible case. If we consider the probability distribution in the beginning(P) as [50% 50%] and in the end of reverse experiment(Q) as [50% 50%]. If P=Q, log(P/Q)=log(1)=0.
DKL(P||Q)=0 if both P and Q are same, which implies the experiment is reversible. Let us look at the second scenario. P =[50% 50%], Q=[33% 66%], which implies:
DKL(P||Q)=50% * log(50%/33%) + 50% * log(50%/66%)= 0.0689
This shows how we can quantify the irreversibility.
What next?
I am a person who likes to tinker with models using numerical experiments. So I might come up with few simulation experiments. Watch out for those articles! :)
References
[0]: KL divergence expalined: A blog article
[1]: Arrow of Time in Active Fluctuations by É. Roldán, J. Barral, P. Martin, J.M.R. Parrondo and F. Jülicher (arXiv:1801.01574 (2018))
[2]: Experiments on the Thermodynamics of Information Processing The Ph.D. thesis of Momčilo Gavrilov
[3]: Irreversibility and Dissipation in Microscopic Systems The Ph.D. thesis of Édgar Roldán
Unfortunately, I cannot really help to clarify your confusion. This is to far from my level of expertise... Sorry. Very nice example with the double well by the way :)
Thank you. The credit of this kind of illustration goes to Momčilo Gavrilov and the team. I adapted it and shared it. I loved their work very much!
Make it 3D and you got a Mexican hat... and then a Higgs boson ;)
Is Mexican hat technically a double well? It's a single well I guess😅
Make it 3D by adding a revolution symmetry around the vertical axis: the double-well becomes a single valley ;)
or there is another way: like this: https://hive.blog/steemstem/@dexterdev/particle-in-a-double-1554311912
but then you have no rotational symmetry, haven't you?
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @steemstem account (for some ROI).
Thanks for using the STEMsocial app, which gives you stronger support. Including @stemsocial as a beneficiary could yield even more support next time.
~~~ embed:1260770034785214465 #posh twitter metadata:ZGV2YW5hbmRfdHx8aHR0cHM6Ly90d2l0dGVyLmNvbS9kZXZhbmFuZF90L3N0YXR1cy8xMjYwNzcwMDM0Nzg1MjE0NDY1ICNwb3NofA== ~~~
Read 66% as 66.66666666 and 33% as 33.333333333. :P
Congratulations @dexterdev! You have completed the following achievement on the Hive blockchain and have been rewarded with new badge(s) :
You can view your badges on your board And compare to others on the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @hivebuzz:
Support the HiveBuzz project. Vote for our proposal!