Saludos y bienvenidos a este blog. En la segunda parte de esta publicación dedicada a los diagramas de fuerza axial, abordaremos la parte matemática de los mismos, donde relacionaremos las cargas externas con la forma del diagrama, a manera de poder caracterizarlo cuantitativamente mediante una ecuación.

En la Parte I se realizó una introducción a estos diagramas y se abordaron desde un punto de vista cualitativo, para así desarrollar una noción general del efecto de las diferentes cargas externas en estos diagramas. En la presente publicación, se hallará la ecuación matemática que describe al diagrama de fuerza axial a través de relaciones diferenciales e integrales con las cargas externas.
Esta serie de publicaciones se centra en los diagramas de solicitaciones de sistemas planos con cargas en su plano y se divide en las siguientes partes:
•Diagramas de fuerza axial (N).
•Diagramas de fuerza cortante (V).
•Diagramas de momento flector (Mf).
•Aplicaciones prácticas de los Diagramas de Solicitaciones.
•Metodología para elaborar los diagramas de solicitación ante cualquier sistema de cargas.
Introducción |
En la Parte I ya vimos como las solicitaciones se generan a partir de un sistema de cargas externo, es decir, no existen las solicitaciones locales sin la presencia de una acción externa. De igual forma, cuando estas acciones externas están presentes, las características de estas determinarán la forma en que las solicitaciones locales o las fuerzas internas “fluyen” a través del elemento.
La acción de tensar una cuerda en sus extremos generará en cualquier punto de la misma una fuerza interna de tracción (tensión) constante, es decir, un diagrama de fuerzas axiales uniforme o rectangular. No podría decirse los mismo de la misma cuerda si esta estuviera siendo tensada desde diferentes puntos a la vez, esto genera internamente variaciones en magnitud de la fuerza axial, haciendo que la forma del diagrama de fuerzas axiales no sea constante (Fig. N°1).
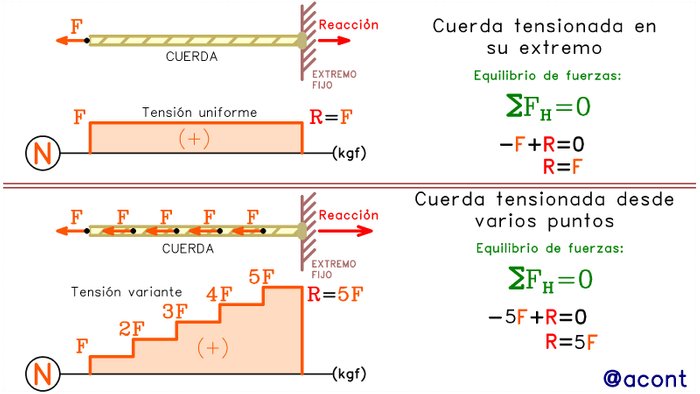
Si asumimos que estas fuerzas puntuales aumentan en número y se colocan muy cercanas entre sí, los saltos en el diagrama se harían mucho más pequeños, haciendo que el diagrama tienda a una línea recta. En el caso anterior, podríamos asumir que las fuerzas puntuales se convierten en una carga distribuida axial uniforme, y ya vimos en la anterior publicación que su efecto en el diagrama es el de generar una variación lineal con pendiente positiva o negativa.
Si logramos encontrar una función matemática que defina la forma de la carga distribuida axial, entonces es posible encontrar a partir de esta una ecuación que describa el diagrama de fuerzas axiales.
Aplicación del cálculo |
Si un elemento se encuentra totalmente comprimido o tensionado desde sus extremos, entonces el diagrama de fuerzas axiales mostrará simplemente un valor constante, es decir, el diagrama será rectangular. En estos casos, no es realmente necesario ningún análisis adicional. Por otro lado, distintas configuraciones de las cargas externas generarán distintas formas en el diagrama y eso lo veremos con detalle a continuación.
En ocasiones, es posible “intuir” de alguna manera la forma del diagrama de fuerza axial (o de cualquier solicitación) y determinar sus valores tal como se hizo en la publicación anterior, no obstante, esto se basa en observaciones cualitativas basadas en la experiencia de cualquier persona que se desenvuelve con facilidad en este ámbito. Para un estudiante que recién empieza a conocer los diagramas de solicitaciones, es necesario empezar a entender el trasfondo matemático y recurrir a procedimientos más exactos para poder empezar a elaborarlos con eficacia. Esto lo podemos conseguir a través del cálculo.
Modelado matemático de las cargas externas
Como mencioné anteriormente, las cargas externas influyen directamente en las características del diagrama de cualquier solicitación, y para estudiar esto a detalle, es necesario discretizar matemáticamente a las cargas externas a través de una función q(x). Esta función no incluye a las cargas puntuales sino a las distribuidas, puesto que las puntuales, como ya vimos, solamente generan discontinuidades verticales en el diagrama.
El eje “x” representa al elemento en sí (miembro lineal) y tiene su origen en el punto donde la carga distribuida inicia (de izquierda a derecha).
Ya que estamos hablando del diagrama de la fuerza axial, nos interesa la función matemática de la carga distribuida en la dirección “N”, es decir, la función qN(x). Aunque estas cargas pueden adoptar la forma de cualquier función f(x), generalmente se presentan en tres variantes:
•qN(x)=0 (no existe carga externa distribuida en el intervalo).
•qN(x)=constante (carga distribuida axial uniforme).
•qN(x)=ax+b (carga distribuida axial con variación lineal).
Es preferible expresar siempre la ecuación qN(x) en función de la ecuación de la recta (qN(x)=ax+b) y aplicar casos particulares tal como se muestra en la Fig. N°2:
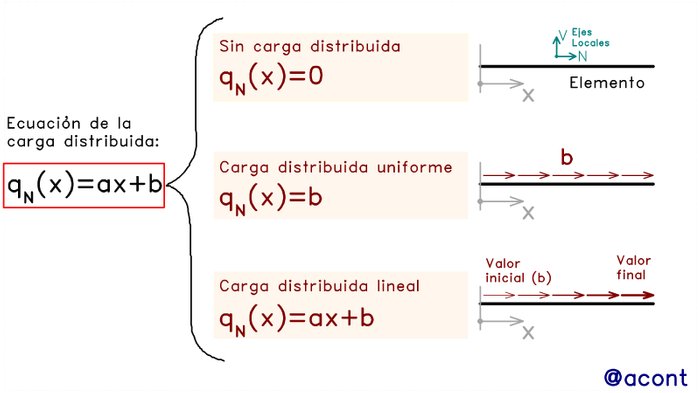
Pero ¿Cómo se determinan los valores de “a” y “b”?
Antes de proseguir a definir lo que será el diagrama de fuerzas axiales de manera analítica a través del cálculo, es muy importante que el estudiante sepa obtener de manera correcta los valores de “a” y “b” en los casos donde la carga distribuida axial se hace presente.
Para obtener el valor de “b”, se tiene una regla bastante sencilla: ”b” será positivo si la carga distribuida axial se orienta hacia la izquierda, y va a depender de si se trata de una fuerza distribuida axial de valor constante o de variación lineal. El valor de “a” se obtiene evaluando la función qN(x)=ax+b para el valor en el extremo derecho de la carga distribuida axial.
Dicho de otra forma, si tenemos una carga distribuida que empieza en un punto inicial Xi=0 m con un valor inicial “qi”, y termina en un punto final Xf=5 m con un valor final “qf”, entonces el valor de “b” lo obtendremos mediante la ecuación qN(0)= qi, y luego, ya conocido “b”, se determina “a” mediante la ecuación qN(5)= qf.
Esto lo podemos entender mucho mejor en los ejemplos prácticos de la siguiente Figura:

En el segundo caso de la Figura N°2 ¿Cómo sabemos que los valores de “a” y “b” son correctos? Una simple evaluación para X=5.00 m nos arroja un valor de 500 kgf/m, lo cual se comprueba al observar la carga distribuida. El error más común en los estudiantes es colocar signos erróneos en los valores de “a” y “b” en la ecuación q(x), teniendo un efecto negativo en los resultados a obtener más adelante.
Es por ello que personalmente recomiendo el método de evaluar la función qN(x)=ax+b tanto para el extremo inicial como para el extremo final de la carga, teniendo en cuenta que el signo positivo únicamente se da cuando la carga axial se dirige hacia la izquierda. Esto nos ayuda a llegar de manera más directa y efectiva a los valores correctos de “a” y “b”.
Se podría relacionar la ecuación qN(x) con la forma de la ecuación de una recta, donde “a” es la pendiente y “b” el valor inicial. El resultado obtenido en el segundo caso de la Fig. N°3 refleja una pendiente negativa, y lo podemos ver en la carga distribuida, ya que su valor disminuye en magnitud hacia la izquierda.
Hallando la ecuación del diagrama de fuerzas axiales: N(x)
La aplicación del cálculo se basa en que existe una relación directa entre el área ocupada por la distribución de cargas axiales y el valor de la fuerza axial en determinado punto interno de un elemento [1]. Por consiguiente, al tratarse del área debajo de una curva (en este caso la ecuación de la carga distribuida) para cualquier elemento diferencial, el uso de la integración es necesario.
Ahora que ya sabemos cómo discretizar matemáticamente la carga distribuida axial, podemos abordar la parte más importante, lo que define matemáticamente el diagrama de fuerza axial. La ecuación del diagrama de fuerza axial N(x) es el resultado directo de integrar la ecuación qN(x) respecto a “dx” el cual representa un segmento diferencial de la longitud de la barra o elemento lineal.
La importancia de encontrar los valores correctos de “a” y “b” radica en que de ellos dependen la realización de un diagrama de solicitación sin errores. Podemos entonces expresar a N(x) como la siguiente integral indefinida:
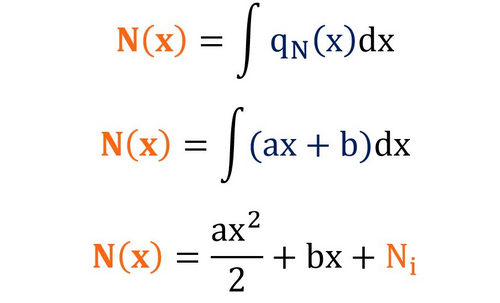
Es evidente que el proceso de integración arrojará una constante. Dicha constante (que se le suele llamar “C” en el estudio del cálculo) podemos denominarla “Ni”, es decir, el valor inicial de la fuerza axial, en el punto inicial del intervalo. Dicho valor de “Ni” siempre es conocido, pues representa el valor de fuerza axial en el extremo izquierdo de la barra producto del despiece y la transformación de reacciones al sistema local.
Para repasar o aprender sobre el cálculo integral, recomiendo las publicaciones realizadas por el Prof. Ing. @carlos84 respecto al Proceso de integración o antiderivación y las Reglas básicas de la integración. Pueden pasar por su blog para ver muchos más artículos referentes al Cálculo a nivel universitario.
Ejemplo N°1
Veamos a continuación un ejemplo práctico en el que se realiza el diagrama de fuerza axial del siguiente elemento (barra) de un sistema isostático (Fig. N°4).

Podemos notar que la barra está sometida a una carga distribuida axial uniforme de 960 kgf/m orientada hacia la izquierda en toda su longitud. Esto matemáticamente se puede expresar de la siguiente forma:
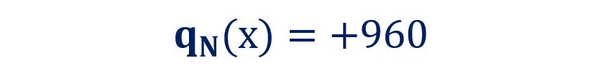
Procedemos a integrar la ecuación de la carga distribuida axial para así obtener la ecuación que define el diagrama de fuerza axial (N(x)):
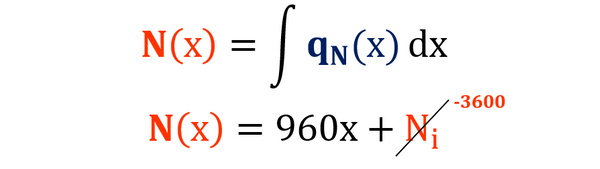
“Ni” corresponde al valor de la fuerza axial inicial, en el extremo izquierdo de la barra (definido así por los ejes locales asignados). En este caso, tenemos un valor de 3600 kgf que se encuentra causando compresión a la barra en su extremo izquierdo. Recordemos que los diagramas de solicitaciones siguen la convención de signos de las solicitaciones locales, en la que la fuerza axial se considera positiva si se tensiona el elemento. Debido a esto, el valor inicial de la ecuación, y por lo tanto del diagrama, será de Ni=-3600 kgf.
Si graficamos esta ecuación en el diagrama, fijando el extremo izquierdo como nuestro origen de coordenadas, tendremos nuestro diagrama de fuerzas axiales (Fig. N°5):
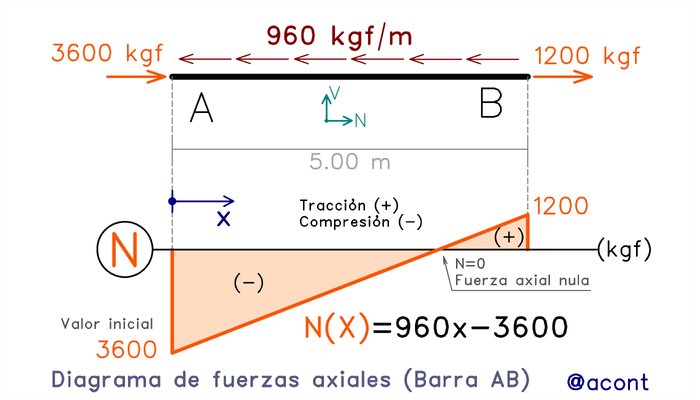
¿Cómo sabemos que la ecuación hallada es correcta? Si evaluamos N(x) para un valor de X=5.00 m, obtendremos el valor de la fuerza axial existente en el extremo derecho, indicando incluso su signo. En el extremo derecho tenemos una fuerza de tracción (tensión) de 1200 kgf, lo cual se comprueba al realizar la evaluación, ya que esto nos arroja un valor de +1200 kgf.
El diagrama de la Fig. N°5, presenta un punto con la singularidad de que la fuerza axial allí es nula. Para hallar la ubicación de este punto, igualaremos la ecuación N(x) a cero, para despejar el valor de “x” correspondiente:
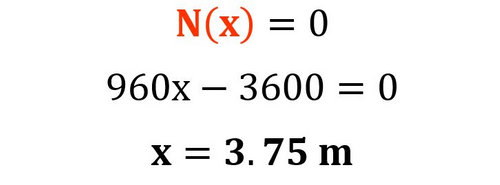
De esta manera, encontramos que el punto donde N=0 se encuentra a 3.75 m del punto inicial (extremo izquierdo).
Ejemplo N°2
Veamos ahora un ejemplo en el que la carga distribuida presenta variación lineal, alterando los valores del ejemplo anterior (Fig. N°6):
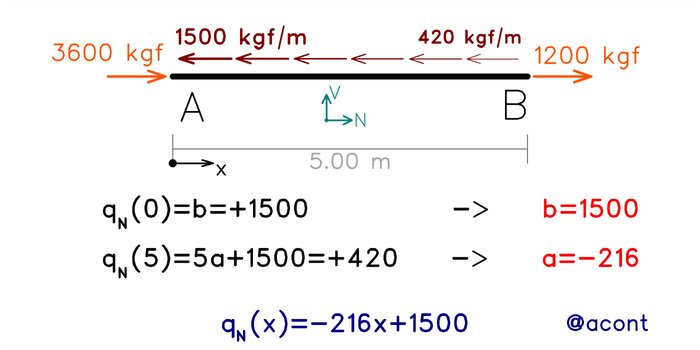
Luego de hallada la ecuación de la carga “qN(x)”, se procede con la integración, sabiendo que el valor inicial será de Ni=-3600 kgf (compresión en el extremo izquierdo):
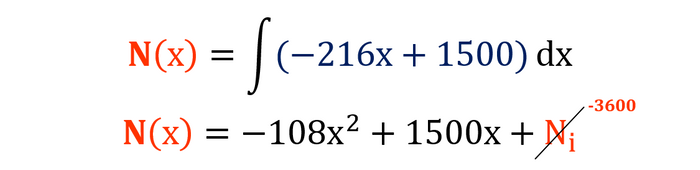
Finalmente, representamos esta ecuación gráficamente, comprobando que al evaluar N(x), para un valor de x=5.00 m, obtenemos el valor existente en el extremo derecho (Fig. N°7):
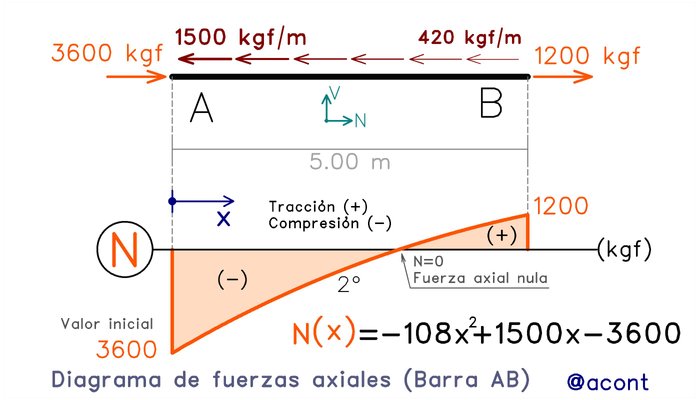
Podemos observar la forma parabólica del diagrama de fuerza axial. Hemos caracterizado matemáticamente la forma de la parábola a partir de una ecuación que define a la carga distribuida lineal. El primer término es negativo, por lo cual la parábola abre hacia abajo.
Para hallar el punto donde la fuerza axial es nula, se procede de igual forma que el ejemplo anterior, pero en este caso, obtendremos dos valores solución ya que se trata de una ecuación cuadrática:

Nos quedamos con el primer valor ya que se encuentra dentro del dominio de interés (0.00 m≤x≤5.00 m). El segundo valor corresponde al otro punto donde la parábola intercepta el eje x (Fig. N°8):
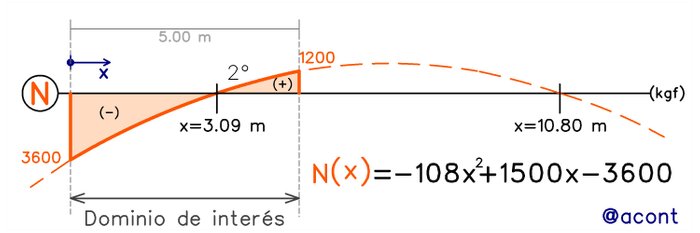
Este otro punto, sin embargo, carece de interés práctico, ya que se encuentra fuera de los límites del elemento estudiado, pero nos permite ver con mayor claridad el comportamiento parabólico del diagrama.
Ejemplo N°3: discontinuidades
Se debe tener presente que la ecuación N(x) describe matemáticamente el diagrama en determinado intervalo, y no necesariamente a toda la barra o elemento lineal.
Los intervalos o tramos vienen dados por discontinuidades en el diagrama, es decir, fuerzas puntuales o cambios en la forma de la carga distribuida. Esto genera cambios en el valor inicial “Ni” y en la ecuación qN(x) para cada nuevo intervalo respectivamente. Por esta razón, la ecuación N(x) será diferente para cada tramo.
Para cada intervalo, se reinicia el origen del eje “x”, así que cada tramo, las ecuaciones tendrán su valor inicial correspondiente. En la Figura N°9 podemos observar lo mencionado anteriormente:
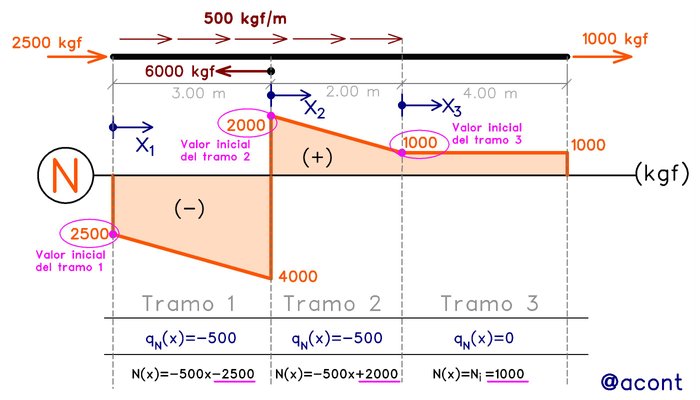
Esta es la ciencia detrás de los diagramas de solicitaciones. Es una relación matemática expresada en una gráfica entre las cargas externas y las fuerzas internas que actúan dentro de un elemento de un sistema isostático (o cualquier sistema estructural).
Aportes de esta publicación
| El diagrama de fuerzas axiales es una representación gráfica de la magnitud de la fuerza longitudinal a lo largo de todo un elemento lineal, ya sea una barra de un sistema isostático, o un miembro de un sistema estructural. En Estática Aplicada, el estudiante adquiere las herramientas matemáticas para elaborar dichos diagramas a partir de una relación directa con las cargas externas. Por ello, esta publicación aborda en profundidad el proceso de elaboración de estos diagramas, detallando procedimientos y casos particulares, para un mayor alcance por parte del estudiante. Es importante la correcta caracterización matemática de las cargas externas, aprendiendo a encontrar la ecuación que define a las cargas distribuidas, y entendiendo el efecto de las cargas puntuales y otras discontinuidades en el diagrama. Por ello hago énfasis en encontrar la ecuación de la carga distribuida a través de la evaluación y una convención de signos particular (izquierda (+), derecha (-)), ya que nos evita procedimientos confusos que puedan llevar a errores en los valores de “a” y “b”. El uso del cálculo para caracterizar matemáticamente el diagrama de fuerza axial es un tema poco abordado en la bibliografía disponible, ya que esto se suele dejar para las solicitaciones de fuerza cortante y momento. Mediante esta publicación se aporta material didáctico que representa la elaboración de los diagramas de fuerza axial en el ámbito académico. |
Referencias Bibliográficas
[1]Rodríguez, Iván. (2003). Estática de las Estructuras. (p. 112, 115, 117-121).Fuente
Material recomendado
•Las Ecuaciones de Equilibrio Estático y algunas aplicaciones en la Ingeniería Civil
•Estática Aplicada: transformación de reacciones al sistema local en barras inclinadas
•Estática Aplicada | Proyección de cargas externas al sistema local de solicitaciones
•Estática Aplicada. Diagramas de Solicitaciones: Fuerza Axial Parte I
Imágenes y ecuaciones de autoría propia realizadas mediante LibreCAD y Microsoft PowerPoint. Gif creado mediante Photoscape.
Publicado mediante la dApp STEMsocial |
Visite la comunidad StemSocial y las etiquetas #STEMsocial y #STEM-espanol para encontrar contenido de calidad referente a Ciencias, Tecnología, Ingeniería, Matemáticas (STEM por sus siglas en inglés) y otros tópicos relacionados. STEMsocial es una comunidad con cuatro años de trayectoria conformada por autores de todo el mundo en la que se comparte y apoya la difusión de contenido STEM de calidad entre sus usuarios.
| Invitación al servidor de Discord de STEM-espanol: https://discord.gg/UJwQXWP | Registro en Hive |
Excelente publicación amigo, tomando en consideración tantos aspectos importantes dentro de tu publicación, voy a comentar sobre esta:
Suele ser muy interesante que el valor de la constante de integración C se denote como Ni, y ademas que este sea representativo para indicar el valor inicial de la fuerza axial del sistema y los componentes que actúan en la estructura.
Gracias por la mención amigo @acont, te recomiendo estar atentos ya que pronto voy a estar en las aplicaciones de la integral que son diversas, quizás una de ellas te llame la atención que es cálculo de masa y centro de masa con integrales.
Saludos amigos y gracias por compartir este post de calidad con toda la comunidad hive.
Gracias por la reseña compañero @carlos84, en definitiva el cálculo integral nos ayuda bastante en estos diagramas.
Creo que olvidé mencionar porqué "C" se denomina "Ni". Eso es porque al evaluar N(x) para x=0, solo nos quedaría N(0)=C, entonces, para x=0 tendríamos el valor de fuerza axial en el extremo izquierdo, el cual sería nuestro valor ya conocido del despiece. Por ello hago la igualdad C=Ni.
Estaré atento a tus futuras publicaciones sobre el cálculo integral para posibles aplicaciones en ingeniería civil. Saludos!
Gracias por la visita estimado @rbalzan79, saludos.
#POSH
Compartido en Twitter
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Thanks for using the STEMsocial app and including @stemsocial as a beneficiary, which give you stronger support.
Thanks for the support #STEMsocial
Excelente post me agrado mucho saludos
Saludos! gracias por la apreciación.😁
Verdaderamente interesante, este material está bueno para usarlo en algunas clases, los ejemplos son fantasticos y muy fácil de entender.. Gracias por esto @acont
Saludos @carloserp-2000! es material didáctico dedicado a estudiantes de Ing. Civl y también cualquier persona interesada en el área, los estudiantes suelen sufrir un poco porque algunas cosas son explicadas "a medias" o no aparecen en las fuentes disponibles. Gracias por la visita.
Saludos @acont, un trabajo magistral realizas, la imágenes son excelentes y el contenido bien explícito dónde logras demostrar los amplios conocimientos en el área, te felicito amigo, seguimos en comunicación !👍
Gracias por la visita a mi blog @amestyj, siempre busco que el contenido sea amigable para el estudiante y para cualquier persona en general, de esta manera lo que normalmente es un poco difícil de entender a primera vista, se hace más accesible, dando lugar a un mayor alcance . Saludos!
Excelente trabajo amigo @acont. Fue un placer para mí leer este post. Muy bien redactado y presentado. Excelente material para los estudiantes del área. Mis cordiales saludos.
Congratulations @acont! You have completed the following achievement on the Hive blockchain and have been rewarded with new badge(s) :
You can view your badges on your board And compare to others on the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @hivebuzz:
Support the HiveBuzz project. Vote for our proposal!
Congratulations @acont!
You raised your level and are now a Minnow!
Do not miss the last post from @hivebuzz:
Support the HiveBuzz project. Vote for our proposal!