¡Saludos y bienvenidos a este blog! Continuando con el contenido relacionado a los Diagramas de Solicitaciones, en esta ocasión empezaremos a abordar los Diagramas de Fuerza Cortante, luego de haber abordado los de fuerza axial en las dos anteriores publicaciones.

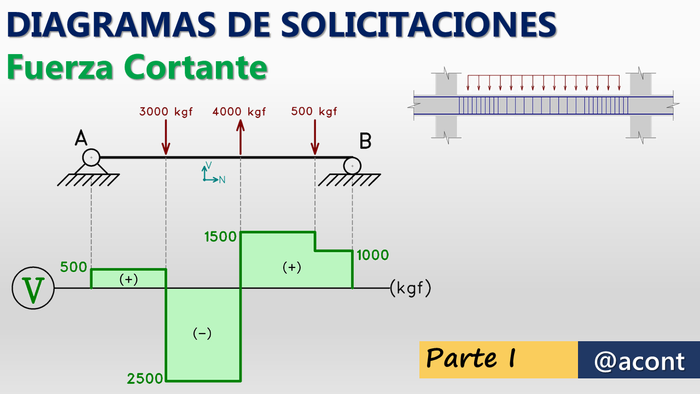
En esta serie de publicaciones, tenemos los siguientes tópicos:

•Diagramas de fuerza axial (N).

•Diagramas de fuerza cortante (V).

•Diagramas de momento flector (M_f).

•Aplicaciones prácticas de los Diagramas de Solicitaciones.

•Metodología para elaborar los diagramas de solicitación ante cualquier sistema de cargas.

Estos diagramas siguen la representación gráfica de las solicitaciones en sistemas planos con cargas en su plano. Las solicitaciones para cargas perpendiculares al plano serán abordadas a futuro.

Introducción

En Estática Aplicada, se pone en práctica el análisis de sistemas isostáticos, calculando primero sus reacciones externas, luego las internas mediante un despiece de sus elementos lineales (“barras” o chapas), posteriormente, luego de realizar un par de procedimientos intermedios si es necesario (proyectar reacciones y cargas externas al sistema local de cada barra), se realizan los diagramas de solicitaciones de sus miembros (barras), con el fin de analizar cómo responde dicho sistema ante las cargas externas impuestas.

Esto corresponde una práctica inicial en el proceso de enseñanza en el área de Ingeniería Estructural para el estudiante, y un primer acercamiento al proceso de estudiar cómo responde un sistema estructural ante cargas impuestas y cómo utilizar esta información para su diseño.

Podemos definir la fuerza cortante (o de cizallamiento) como la fuerza que se genera en una sección transversal de una viga recta, y es la suma algebraica de las componentes que actúan transversalmente al eje de la viga, de todas las cargas y reacciones aplicadas a la parte de la viga a un lado u otro de esta sección o corte transversal [1]. Aunque este concepto anterior se refiere a vigas rectas, la fuerza cortante es una solicitación (reacción interna) que se puede generar en cualquier elemento o miembro lineal si las cargas externas actúan de manera perpendicular a su eje longitudinal. Es por ello que tenemos para cada miembro del sistema unos ejes locales, uno en dirección longitudinal (N) y otro en dirección perpendicular (V).

Cabe volver a mencionar la convención de signos para las solicitaciones locales abordada en este artículo, donde si tomamos un elemento diferencial de un miembro del sistema isostático, las fuerzas de corte en sus extremos deben hacerlo “rotar” en sentido horario para considerar que la fuerza de corte es positiva (Fig. N°1).

_{Figura N°1}
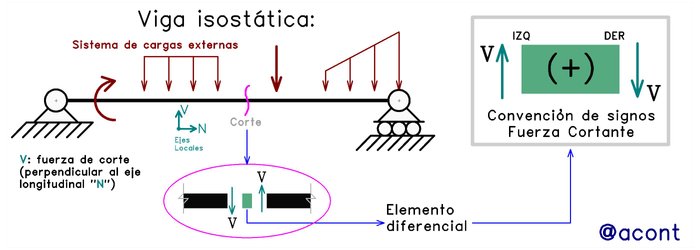
Pero ¿Cómo se aplica esto? Esta convención de signos es menos evidente que la utilizada para la fuerza axial, donde simplemente distinguimos entre tracción (tensión) o compresión. Más adelante podremos comprender mejor el signo de esta solicitación, ya que suele ser más evidente cuando ponemos en práctica la realización de los diagramas de fuerza cortante.

Introducción a los Diagramas de Fuerza Cortante

El objetivo de estos diagramas es mostrar de manera gráfica la variación de la magnitud de la fuerza cortante a lo largo de todo el elemento o miembro de un sistema isostático. Exactamente como sucede con las fuerzas axiales, las características del sistema de cargas externo van a incidir en la forma del diagrama de fuerzas cortantes.

Tal como fue descrito en la definición anterior para las fuerzas cortantes, si no existen cargas externas, no existen solicitaciones, ya que, al realizar un corte en cualquier punto del elemento o barra, al realizar la sumatoria de fuerzas, la fuerza de corte interna sería nula para conservar el equilibrio estático. En cambio, si existe un sistema de cargas externas (en dirección del eje local “V”), es posible obtener un valor dado de la fuerza cortante en determinado punto arbitrario.

Veamos un ejemplo simple de sistema isostático, dado por una viga simplemente apoyada horizontal sometida a cargas puntuales verticales (Fig. N°2):

_{Figura N°2}
En la figura anterior, luego de hallar las reacciones externas, se realiza un corte arbitrario a 5.00 m del extremo izquierdo, y una sumatoria de fuerzas en el lado izquierdo del mismo nos arroja una fuerza de corte interna de 1500 kgf hacia abajo. El mismo resultado con signo opuesto debe de obtenerse en el lado derecho del corte (de lo contrario, el cálculo de las reacciones externas se hizo incorrectamente).

Debe notarse que no importa la ubicación del punto de corte, el resultado obtenido solo depende de las cargas externas que aparezcan a cada lado del corte realizado. Si hubiéramos realizado el corte un poco más a la izquierda o la derecha, el resultado sería igual, al menos que el corte se ubique antes o después de una fuerza puntual dada.

Pero para obtener un estudio completo de la magnitud de las fuerzas cortantes en toda la viga, se debe realizar esta sumatoria de fuerzas en diferentes puntos de la misma haciendo diversos cortes, lo cual es poco práctico. Es por ello que los diagramas de solicitación adquieren importancia.

Si realizamos un análisis de la viga, haciendo cortes y separándola en los puntos donde se encuentran aplicadas las fuerzas puntuales, podremos ver que cada porción de la viga está sometida en sus extremos a fuerzas puntuales que podemos verificar si siguen o no la convención de signos antes descrita (haciendo analogía con el elemento diferencial de la Fig. N°1) (Fig. N°3).

_{Figura N°3}
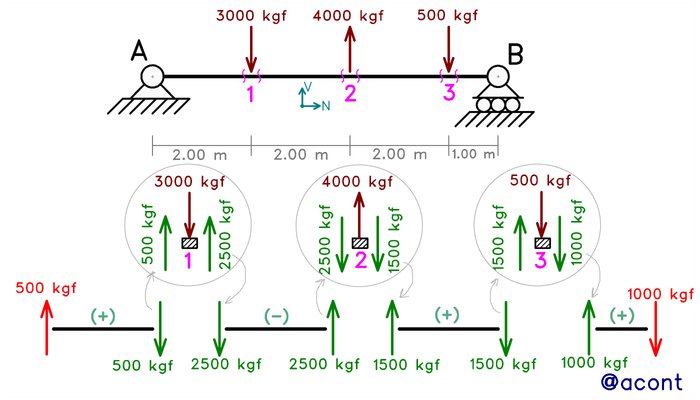
Similar al proceso del despiece de un sistema isostático, podemos analizar por separado el punto donde las fuerzas puntuales son aplicadas, de igual manera a como lo haríamos con una junta de un sistema isostático que recibe una fuerza puntual y se necesita hallar la fuerza equilibrante que se transmite al siguiente elemento.

En la figura anterior, cada porción de la viga muestra fuerzas de corte en sus extremos, lo cual nos lleva a poder graficar el diagrama de corte en cada porción, tomando en cuenta que las fuerzas puntuales externas generan discontinuidades o saltos que son visibles directamente en el diagrama (Fig. N°4).

_{Figura N°4}
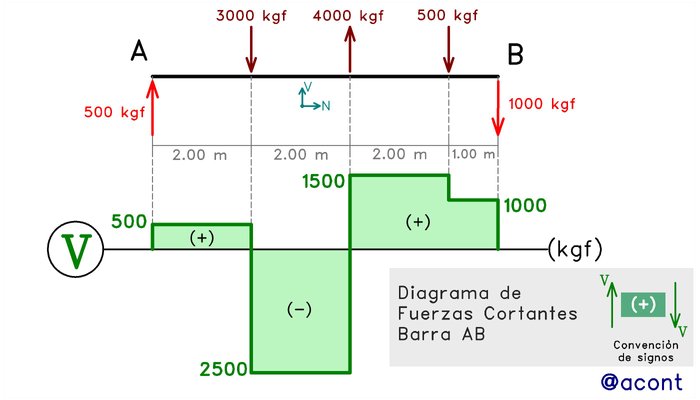
Si solo se presentan fuerzas puntuales externas, resulta evidente que el diagrama de fuerza cortante mostrará valores constantes o diagramas rectangulares, porque como ya mencioné, no importa la ubicación del punto de corte sino de qué cargas están presentes a los lados del mismo.

Cuando entran en juego las cargas distribuidas, se debe poner atención a que porción de estas cargas está siendo tomada en cuenta. Veamos el siguiente ejemplo, donde tenemos una viga simplemente apoyada sometida a una carga distribuida uniforme vertical y una fuerza puntual (Fig. N°5).

_{Figura N°5}
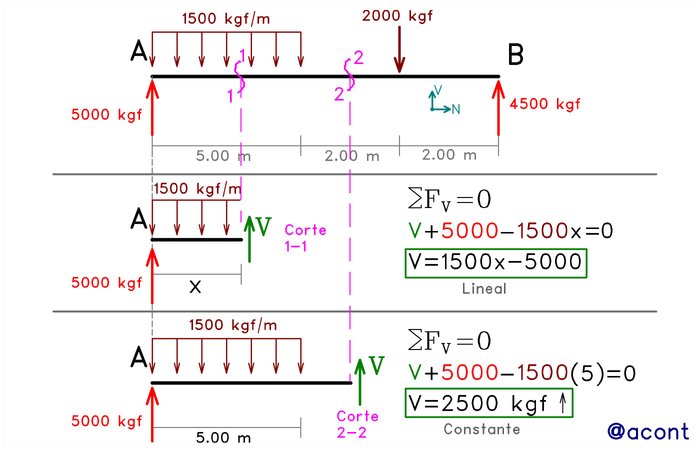
Se han realizado dos cortes en la viga: un corte 1-1, en el cual solo tomamos en cuenta una porción “x” de la carga distribuida; y un corte 2-2, donde tomamos en cuenta por completo a la carga distribuida. El valor a obtener mediante el corte 1-1 dependerá de que tan grande sea la porción tomada en cuenta de la carga distribuida.

En el caso del corte 1-1, la fuerza de corte interna aumenta linealmente a medida que aumenta la distancia “x” tal como lo dice la ecuación obtenida. Este es el principio básico que nos dice que el diagrama de corte presentará variación lineal cuando se presentan cargas distribuidas uniformes.

El diagrama de corte para el ejemplo de la Fig. N°5 se muestra en la siguiente figura:

_{Figura N°6}
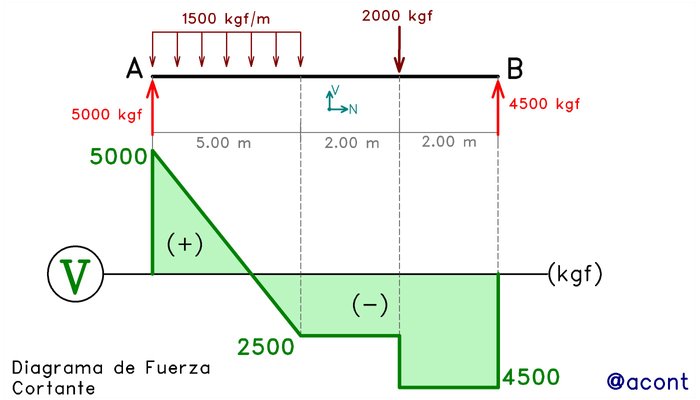
En la siguiente publicación abordaré el uso del cálculo para graficar el diagrama de corte hallando la ecuación matemática que lo define. Por ahora, veremos de forma cualitativa el efecto de diferentes cargas externas en la geometría del diagrama de corte.

Para ilustrar un poco la importancia de la fuerza cortante, el diseño de las vigas en edificaciones de concreto armado toma mucho en cuenta la magnitud de esta solicitación y cómo se comporta a lo largo de ellas. Tomando el caso de carga más simple y común (carga distribuida uniforme, debida al peso propio y demás cargas requeridas para el diseño), el diagrama de fuerzas cortantes mostrará valores máximos en los extremos de viga y valores bajos o nulo en el centro de esta (Fig. N°7).

_{Figura N°7}
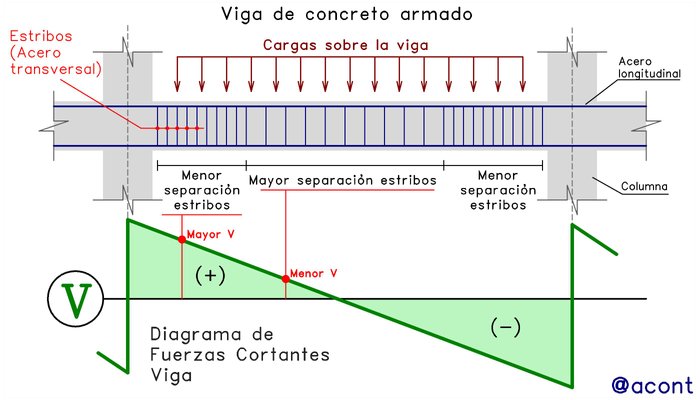
Es debido a esto que en vigas de edificaciones de concreto armado, los estribos (acero transversal de las vigas) se suelen colocar más cercanos en los extremos de viga, mientras que en el centro se suelen colocar más separados, debido a que estos se utilizan, entre otras cosas, para absorber los esfuerzos de corte que se generan en la viga. Esto sería un ejemplo muy simple de diseño del acero transversal de una viga, otros factores se toman en cuenta, como las fuerzas sísmicas y exigencias mínimas de las Normas.

Efectos de cargas externas en la geometría de los diagramas de fuerza axial

Cualquier carga externa que no se encuentre en dirección del eje local “V” no causará efecto alguno en la magnitud fuerzas cortantes internas, por lo tanto, no tienen efecto alguno en el diagrama de esta solicitación.

Los momentos externos que puedan actuar en un elemento de un sistema isostático tampoco generan alteración alguna en las fuerzas de corte. Más adelante, abordaré los diagramas de momento flector, solicitación que si se ve alterada por los momentos externos y esto se podrá apreciar en su diagrama respectivo.

Teniendo esto en cuenta, podemos estudiar el efecto de cargas externas que inciden en la forma del diagrama de corte, las cuales serían: las fuerzas puntuales cuya dirección es perpendicular al eje del elemento o barra; y las cargas distribuidas, uniformes o trapezoidales, que también posean esta dirección.

Las fuerzas puntuales, similar al caso estudiado con las fuerzas axiales, tienen el efecto de generar una discontinuidad en el diagrama de corte. Esto ya lo observamos en la Fig. N°4, pero en la siguiente figura observaremos una imagen animada para distintas magnitudes y sentido de una fuerza externa “F” actuando en la mitad de la barra, generando un salto vertical en el diagrama.

_{Figura N°8}
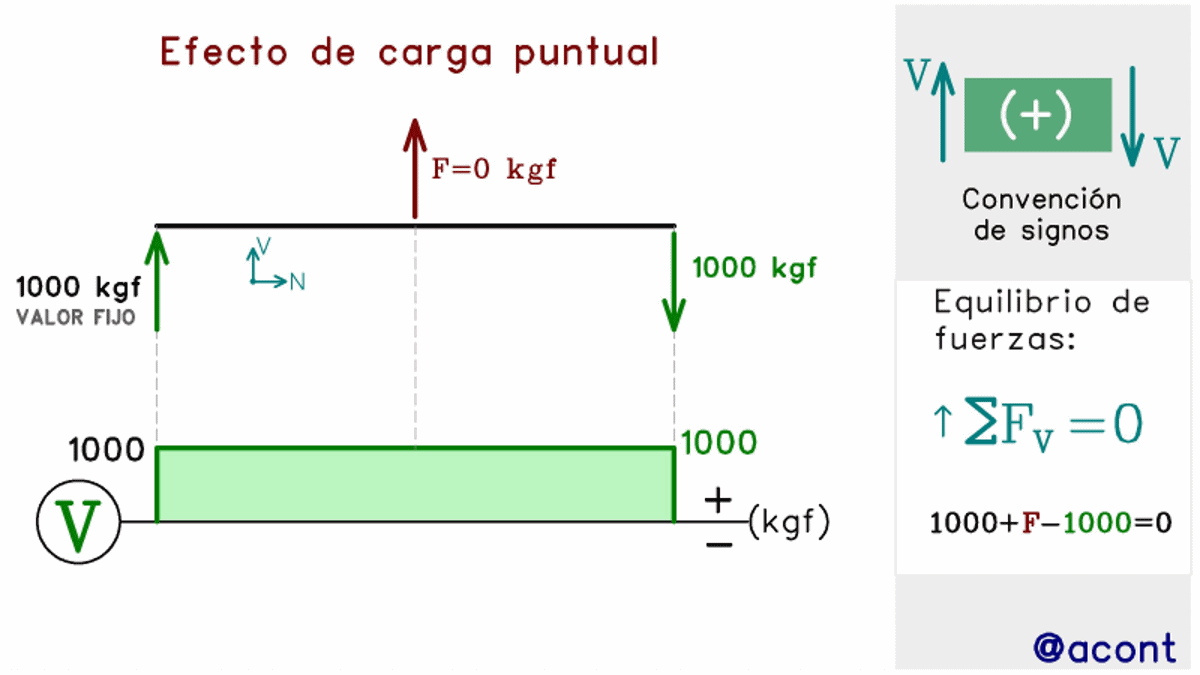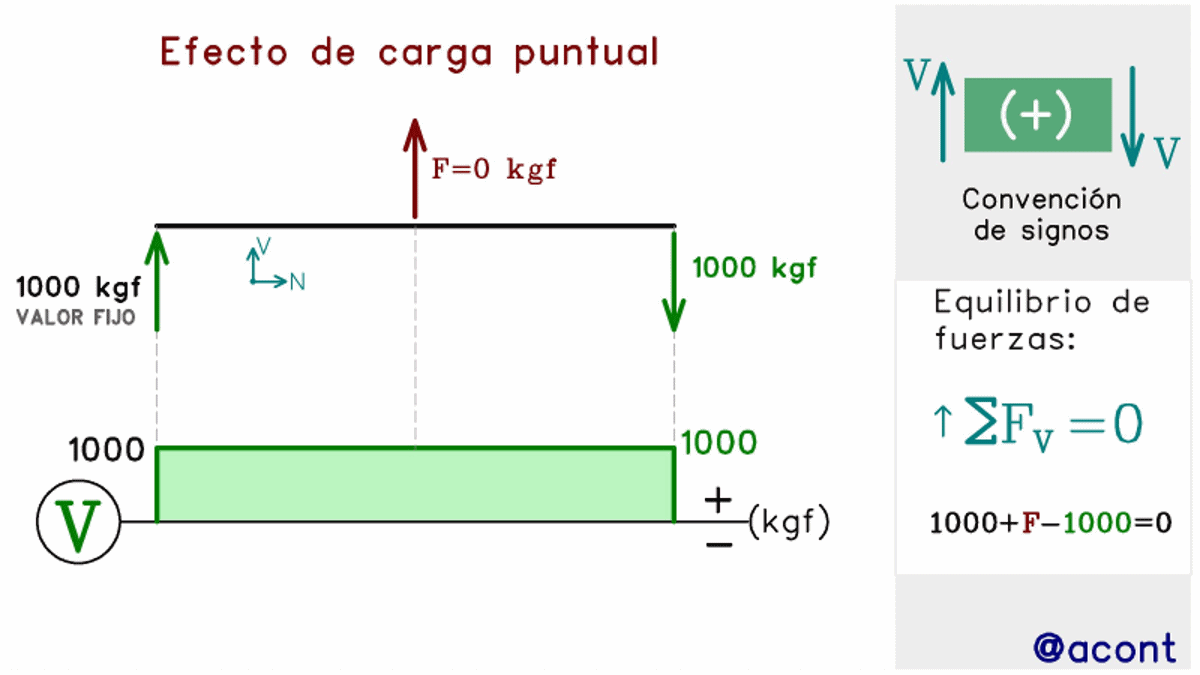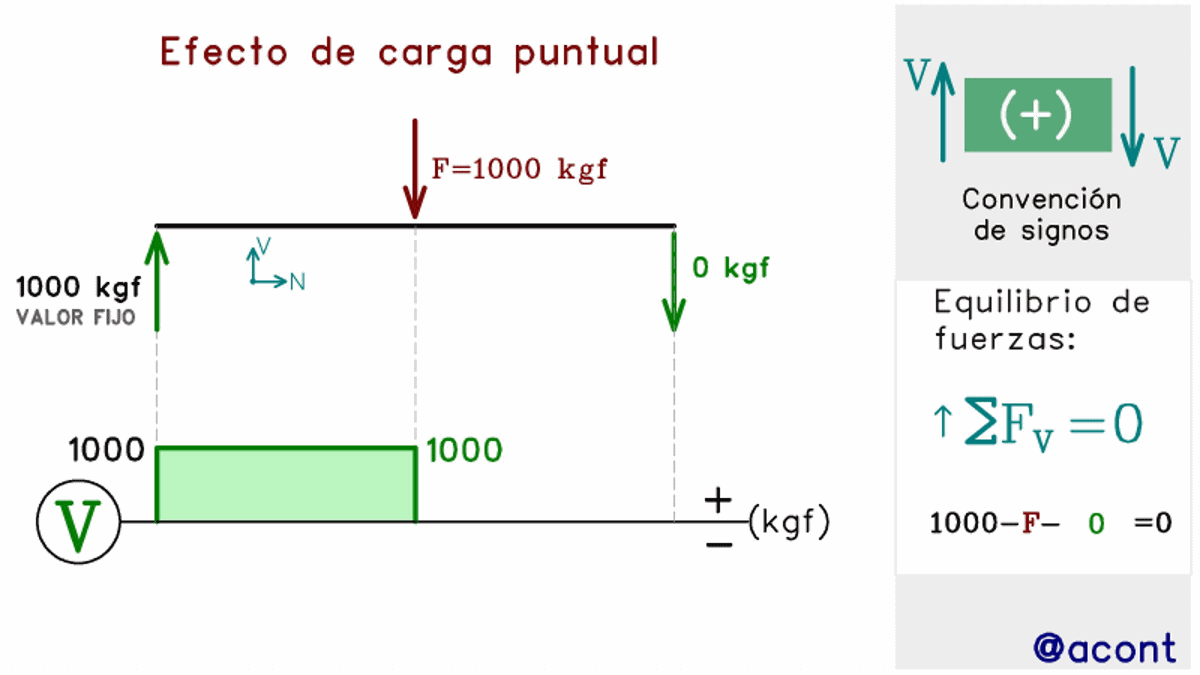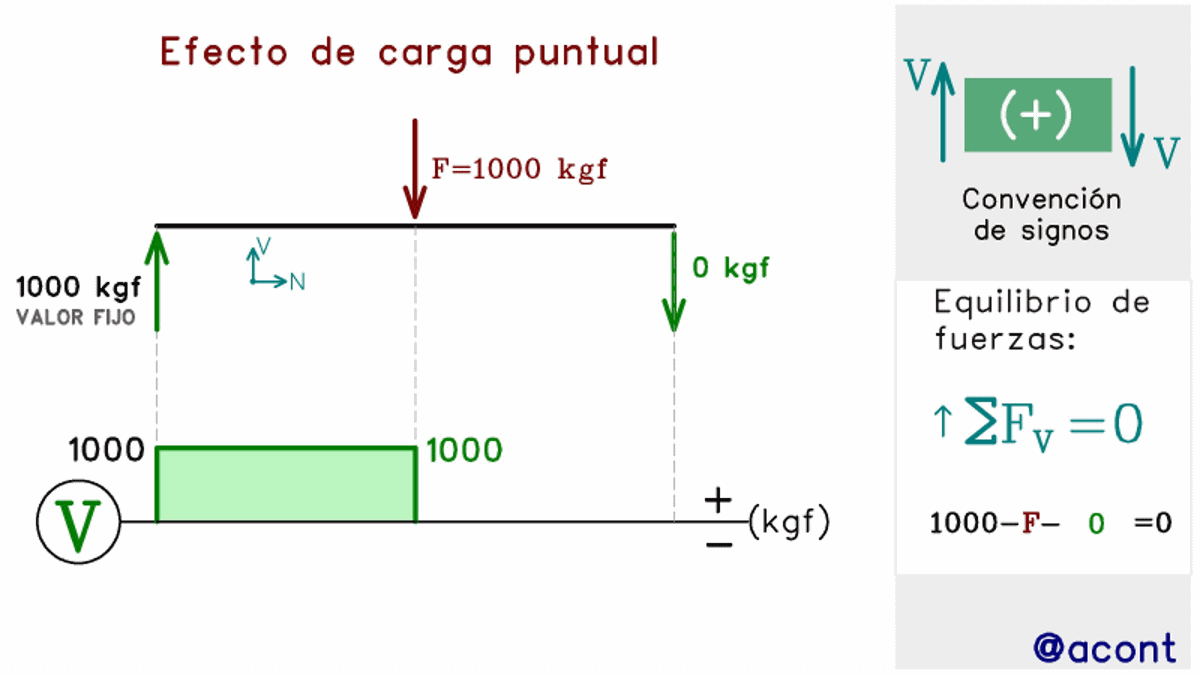
Se ha fijado el valor de la fuerza cortante en el extremo izquierdo, mientras que la fuerza de corte en el extremo derecho variará en su magnitud y sentido para poder mantener el equilibrio estático en la barra.

Ya vimos como la carga distribuida uniforme genera una variación lineal de la magnitud de la fuerza cortante (Fig. N°6). En la siguiente figura animada, veremos con mayor detalle (de forma cualitativa), como la magnitud y sentido de la carga distribuida uniforme inciden en la geometría del diagrama de corte.

_{Figura N°9}
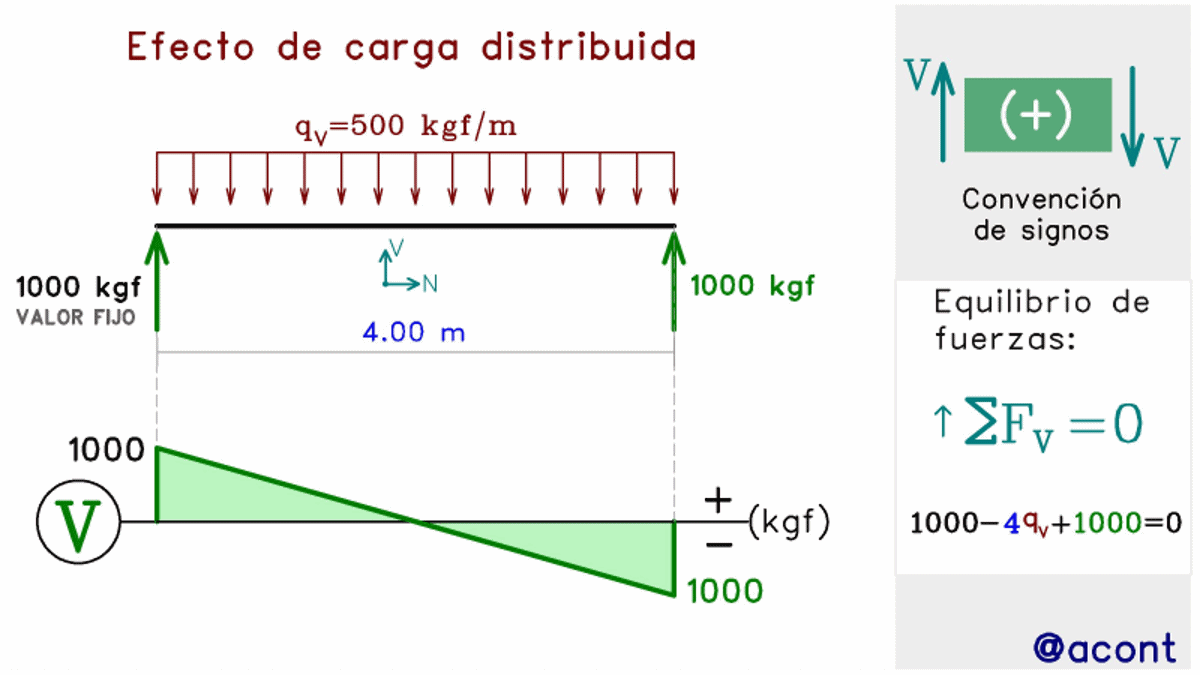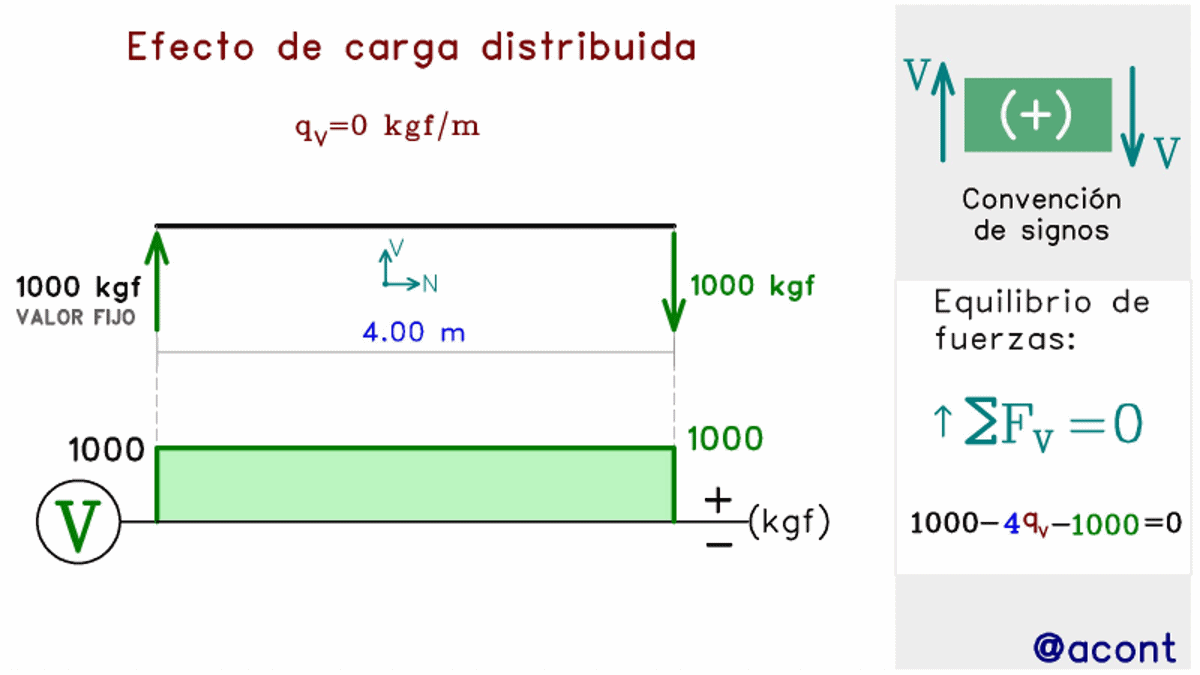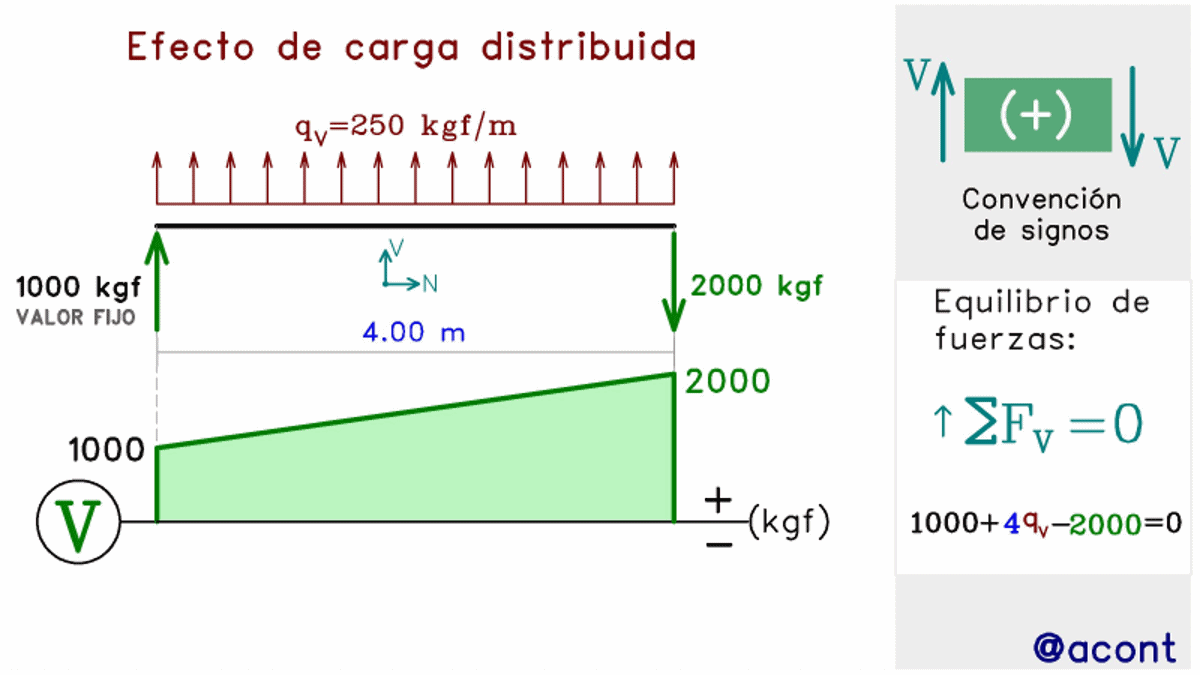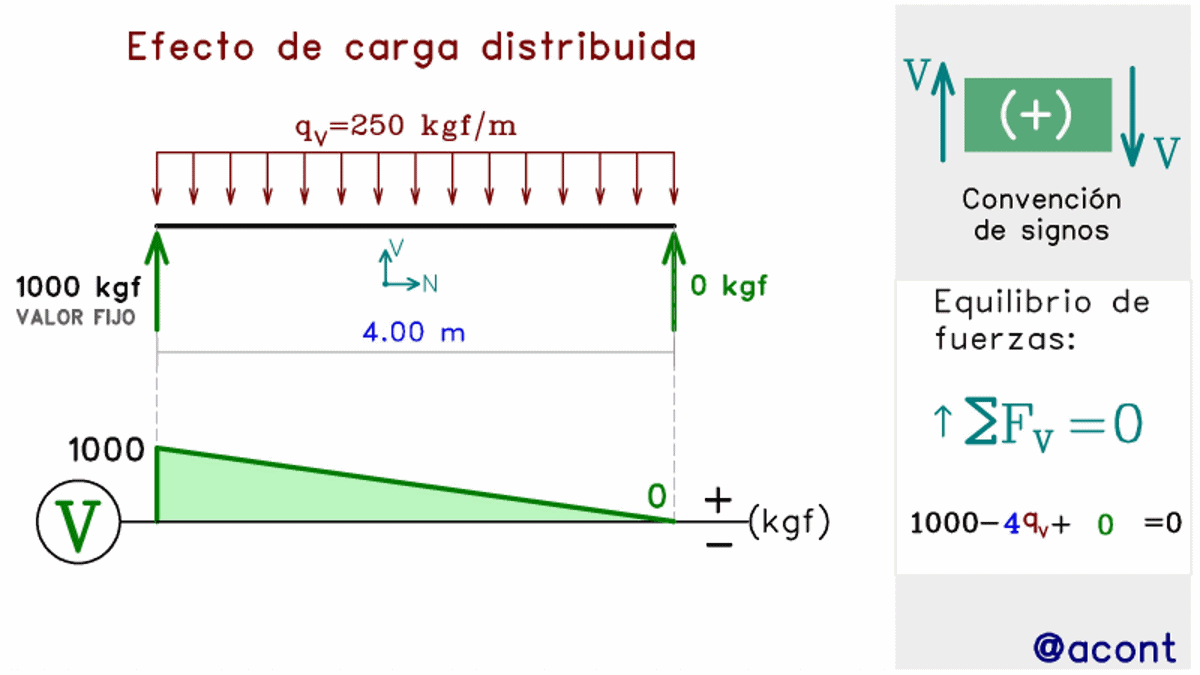
Podemos ver como la carga distribuida al dirigirse hacia abajo, genera una pendiente decreciente hacia la derecha en el diagrama. Si fijamos el extremo izquierdo de la barra como nuestro origen de un par de ejes cartesianos, podríamos decir que la pendiente del diagrama será positiva si la carga distribuida se dirige hacia arriba, y negativa si se dirige hacia abajo.

En el caso de la carga distribuida uniforme en dirección axial (N), teníamos que una orientación hacia la izquierda nos brindaba una pendiente positiva en el diagrama de fuerzas axiales. En el caso de la carga distribuida en dirección cortante (V), los signos de la pendiente siguen una convención más usual (positivo hacia arriba, negativo hacia abajo).

Finalmente, en el caso de la carga distribuida con variación lineal, mejor conocidas como cargas distribuidas trapezoidales, el diagrama seguirá una forma parabólica, cuya geometría depende de las características de la carga trapezoidal. Puede que la carga trapezoidal se oriente hacia arriba o hacia abajo, y de manera simultánea, la carga trapezoidal puede ir de un valor menor a un valor mayor o viceversa (Fig. N°10).

_{Figura N°10}
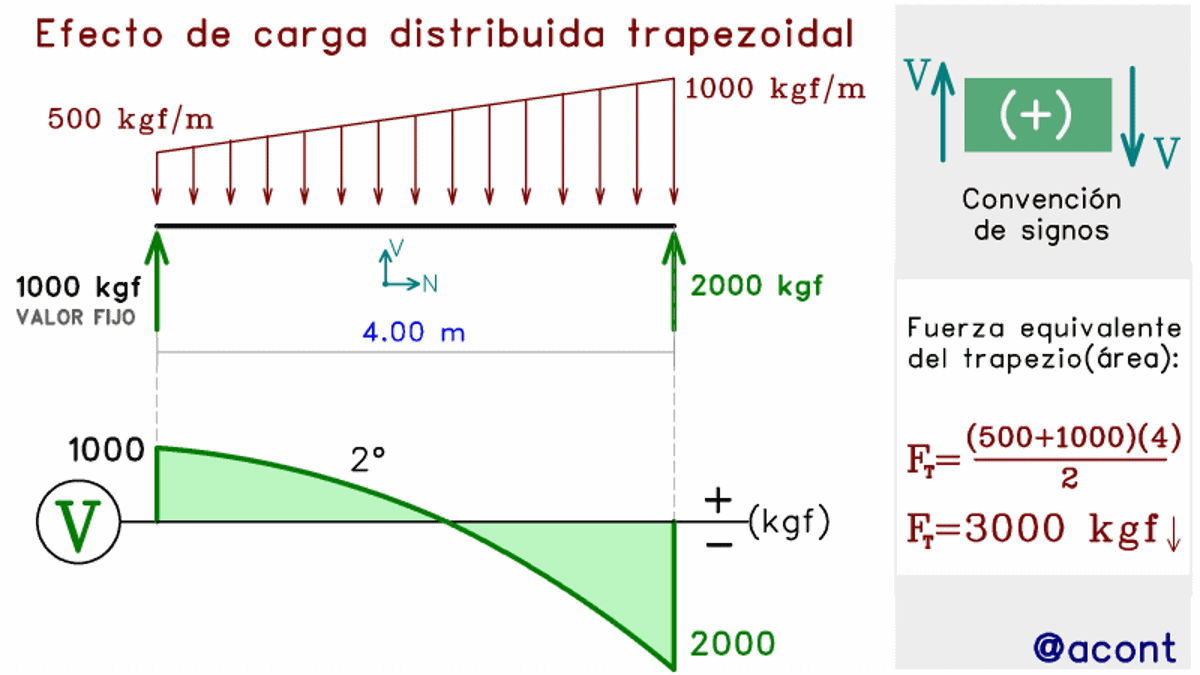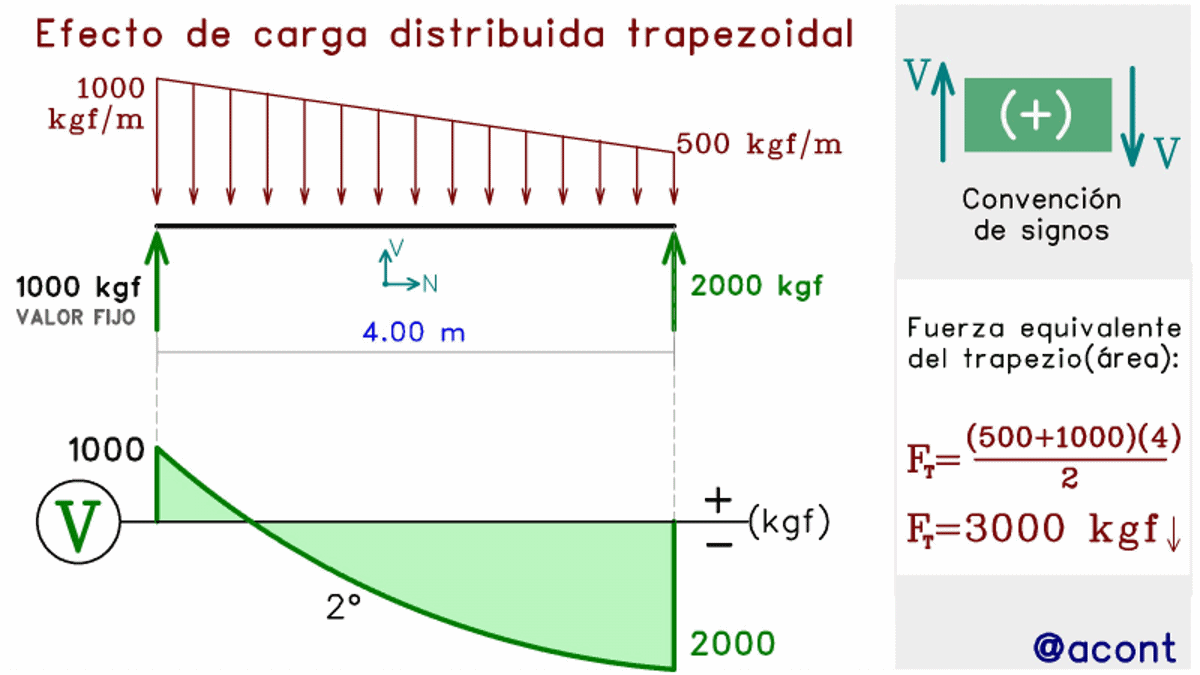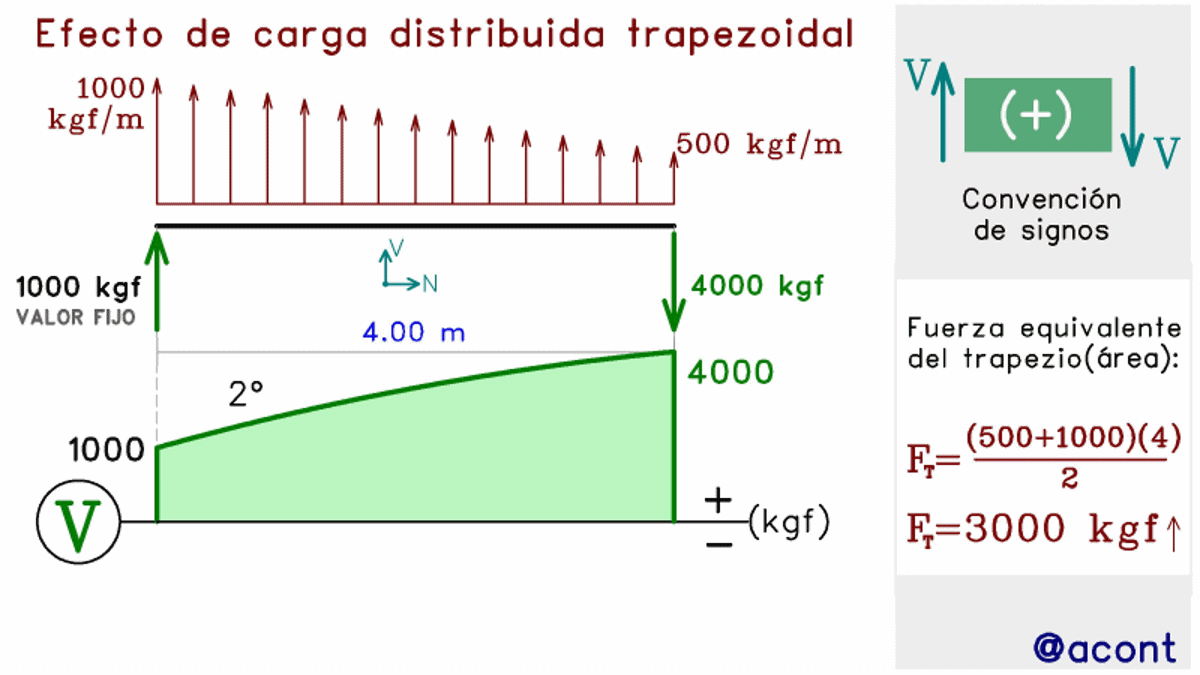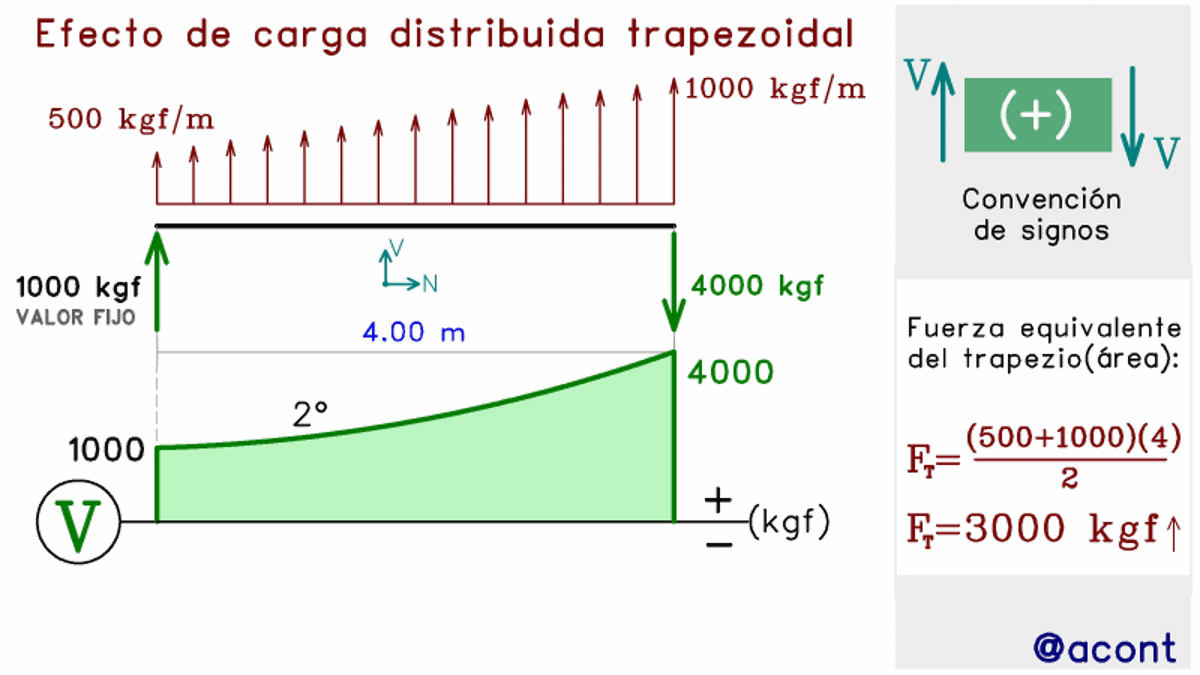
Se observa como tenemos cuatro casos para la forma de la carga trapezoidal, en los cuales la parábola puede abrir hacia abajo o hacia arriba. El valor inicial (el cual se ha fijado) determinará si existe o no corte con la barra, es decir, un punto donde la fuerza cortante es nula (V=0). Para determinar estas características con mayor precisión, necesitaremos de la matemática y el cálculo para poder llegar a una ecuación con la que podamos describir la parábola correspondiente.

Esta es una descripción cualitativa del efecto de las cargas externas en el diagrama de fuerzas cortantes, no existen muchas diferencias respecto a lo abordado respecto a las fuerzas axiales, pero en este caso, estamos ante la presencia de cargas externas más usuales y comunes en la realidad. Es más común en los sistemas estructurales de la realidad, encontrar cargas externas aplicadas de manera perpendicular al eje o superficie de un componente de la estructura, que cargas actuando en dirección longitudinal.

El principio utilizado para la elaboración de los diagramas de fuerza cortante es igual al utilizado para los de fuerza axial, pero en este caso, los diagramas de corte poseen mayor aplicación práctica, puesto que como ya vimos, se utilizan para el diseño de vigas de edificaciones, entre otras cosas. Además, para elaborar los diagramas de momento flector, es necesario pasar primero por la elaboración de los de corte, puesto que ambas solicitaciones están directamente relacionadas, tal como veremos en futuras publicaciones.

Ahora que ya vimos de manera cualitativa cómo se comporta el diagrama de fuerzas cortantes, necesitamos encontrar la forma de cuantificarlo para poder hallar la magnitud de esta solicitación en cualquier punto del elemento. En la siguiente entrada, veremos el abordaje matemático del diagrama de fuerza cortante.

Aportes de esta publicación

La fuerza de corte es una solicitación (fuerza interna) que se genera como respuesta ante la aplicación de cargas externas de manera perpendicular al eje longitudinal de un elemento. Esto es muy común en sistemas estructurales, sobre todo las vigas de una edificación. Es por ello que una representación gráfica de cómo varia esta solicitación es una herramienta que se debe manejar, tanto para abarcar aspectos relacionados al diseño según esta solicitación (por ejemplo, los estribos de una viga de concreto armado), como también para dar paso a la elaboración de los diagramas de momento flector, otra solicitación de suma importancia.

Referencias Bibliográficas

[1]Norris, C. H. y Wilbur, J. B. (1973). Análisis Elemental de Estructuras. Segunda Edición. Libros McGraw-Hill de México. (p. 97-98)._Fuente

[2]Rodríguez, Iván. (2003). Estática de las Estructuras. (p. 112, 119-123)._Fuente

Material recomendado

•Cálculo de reacciones internas (solicitaciones) mediante el Principio del Trabajo Virtual para Cuerpos Rígidos

•Las Ecuaciones de Equilibrio Estático y algunas aplicaciones en la Ingeniería Civil

•Estática Aplicada: transformación de reacciones al sistema local en barras inclinadas

•Estática Aplicada | Proyección de cargas externas al sistema local de solicitaciones

•Estática Aplicada. Diagramas de Solicitaciones: Fuerza Axial Parte I

•Estática Aplicada. Diagramas de Solicitaciones: Fuerza Axial Parte II

Imágenes y ecuaciones de autoría propia realizadas mediante LibreCAD y Microsoft PowerPoint. Gifs creados mediante Photoscape.

Publicado mediante la dApp STEMsocial

Visite la comunidad StemSocial y las etiquetas #STEMsocial y #STEM-espanol para encontrar contenido de calidad referente a Ciencias, Tecnología, Ingeniería, Matemáticas (STEM por sus siglas en inglés) y otros tópicos relacionados. STEMsocial es una comunidad con cuatro años de trayectoria conformada por autores de todo el mundo en la que se comparte y apoya la difusión de contenido STEM de calidad entre sus usuarios.

Invitación al servidor de Discord de STEM-espanol: https://discord.gg/UJwQXWP

Registro en Hive

Estática Aplicada. Diagramas de Solicitaciones: Fuerza Cortante Parte I